Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
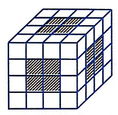
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu.

Đáp án B
Gọi tâm O, O’ lần lượt là tâm của ABCD, A’B’C’D’. Ta có
![]()
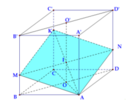
Qua I ta kẻ đường thẳng d song song BD cắt BB', DD' lần lượt tại M, N . Mặt phẳng ( α ) chính là mặt phẳng (KMAN) chia khối lập phương thành 2 phần.
Ta có 2 phần khối đa diện đối xứng qua (AA'C'C) nên ta chỉ cần xét một nửa thể tích của mỗi phần như sau:

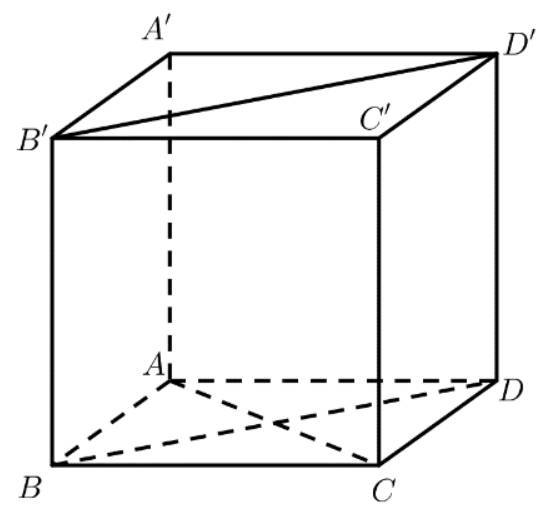
a) Các đường thẳng vuông góc với \(AC\) là: \(B{\rm{D}},B'D',AA',BB',CC',DD'\).
b) Các đường thẳng chéo với \(AC\) là: \(B'D',BB',DD'\).

\( - \;\)Ta có \(\left( {ABB'C'} \right)\;//\;\left( {MNN'M'} \right),\;\left( {ADD'A'} \right) \cap \left( {ABB'A'} \right) = AA',\left( {ADD'A'} \right) \cap \left( {MNN'M'} \right) = MM'\)
suy ra AA'//MM'
Tương tự, BB' // NN'
ABNM.A'B'N'M' có các cạnh bên đôi một song song, (ABNM) //(A'B'N'M')
Suy ra ABNM.A'B'C'M' là hình lăng trụ.
\( - \;\)Ta có: \(\left( {ABB'C'} \right)\;//\;\left( {MNN'M'} \right),\;\left( {ABNM} \right) \cap \left( {ABB'A'} \right) = AB,\left( {ABNM} \right) \cap \left( {MNN'M'} \right) = MN\)
Suy ra AB//MN.
Ta có có AB // MN, BN// AM nên tứ giác ABNM là hình bình hành.
Do đó ABNM.A'B'C'M' là hình hộp.

Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = Q{\rm{R}}\end{array} \right\} \Rightarrow MN\parallel Q{\rm{R}}\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( \alpha \right) \cap \left( {AA'B'B} \right) = NP\\\left( \alpha \right) \cap \left( {CC'D'D} \right) = R{\rm{S}}\end{array} \right\} \Rightarrow NP\parallel R{\rm{S}}\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( \alpha \right) \cap \left( {AA'D'D} \right) = M{\rm{S}}\\\left( \alpha \right) \cap \left( {BB'C'C} \right) = PQ\end{array} \right\} \Rightarrow M{\rm{S}}\parallel PQ\)


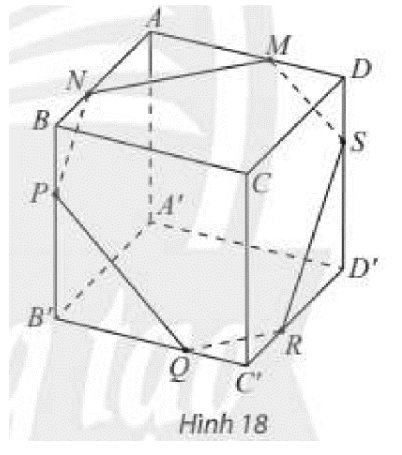
tham khảo:
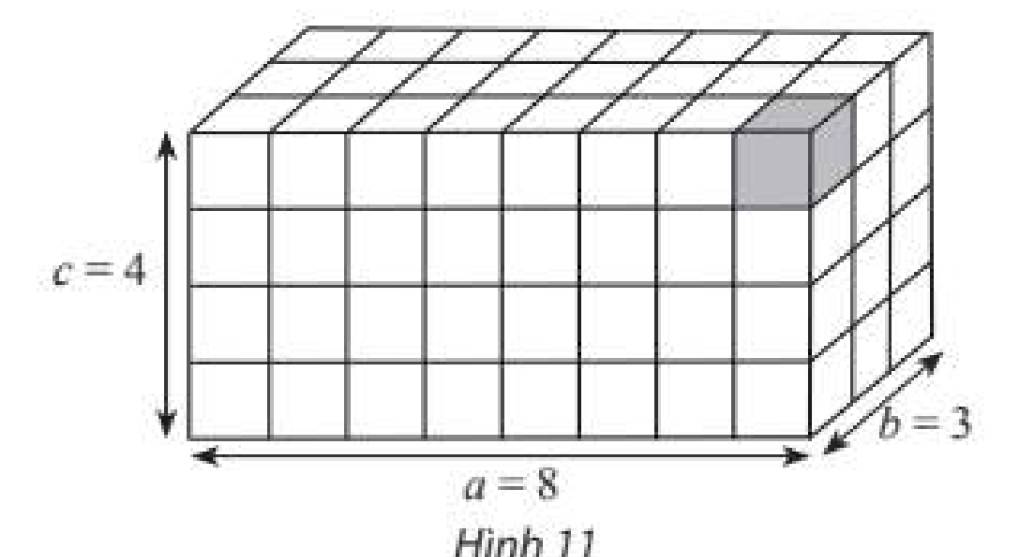
Số lập phương đơn vị là: 8.4.3 = 96