Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
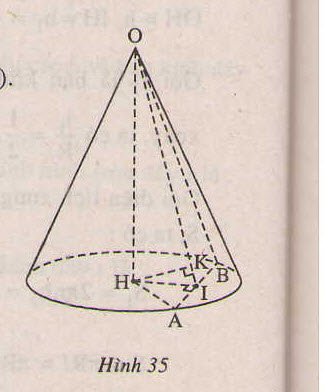
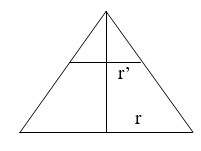
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)

Chọn đáp án A
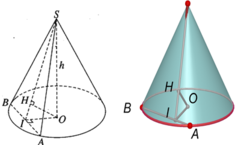
Gọi I là tâm của hình tròn (C) và S là đỉnh của hình nón. Gọi bán kính của hình tròn (C) là r thì
![]()
Trường hợp 1: O nằm giữa S và I.
Chiều cao của hình chóp là SI = SO + OI = x + 6 (cm).
Thể tích khối chóp là V = 1 3 π 36 - x 2 x + 6 cm 3
Xét hàm số f x = 36 - x 2 x + 6 với 0 ≤ x < 6
Ta có f ' x = - 3 x 2 - 12 x + 36
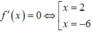
Do 0 ≤ x < 6 nên x = - 6.
Lập bảng biến thiên của hàm số ta thấy f(x) ta thấy f x ≤ f 2 = 256
Suy ra V ≤ V 1 = 1 3 π . 256 = 256 3 π cm 3
Dấu “=” xảy ra x = 2.
Trường hợp 2: I nằm giữa S và O
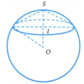
Chiều cao của hình chóp là SI = SO – OI = 6 – x (cm)
Thể tích của khối chóp là V = 1 3 π 36 - x 2 6 - x cm 3 (cm3).
Xét hàm số g x = 36 - x 2 6 - x với 0 ≤ x < 6
Ta có g ' x = 3 x 2 - 12 x - 36 < 0 , ∀ x ∈ 0 ; 6 nên hàm số g(x) nghịch biến trên 0 ; 6 .
Suy ra g x ≤ g 0 = 216
Khi đó V ≤ V 2 = 72 π cm 3 .
Dấu “=” xảy ra khi x = 0.
So sánh hai trường hợp 1 và 2, suy ra thể tích lớn nhất của khối chóp đã cho là V = 256 3 π cm 3 khi x = 2 c m .

Đáp án B
V 1 V 2 = 1 3 π r 2 . S O ' 1 3 π R 2 . S O = 1 2 2 . 1 2 = 1 8 .

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
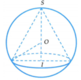
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)


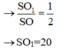




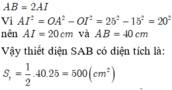

Chọn đáp án A