Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

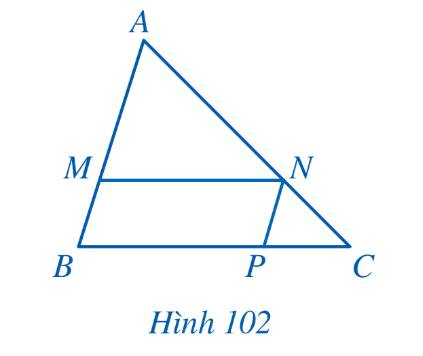
Vì BMNP là hình bình hành nên \(NP\parallel AB\)\(,\,\,MN = BP,\,\,BM = PN\)
\( \Rightarrow \frac{{NP}}{{AB}} = \frac{{CP}}{{CB}}\) (Định lý Thales)
Ta có: \(\frac{{MN}}{{BC}} = \frac{{BP}}{{BC}}\)
Khi đó: \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = \frac{{BP}}{{BC}} + \frac{{CP}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm)

a)
i) Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
ii) Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
b)
i)
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OA'C'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(A'C'//AC\) (định lí Thales đảo)
Vì \(A'C'//AC \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{{AC}}{{A'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'C'}}{{AC}} = \frac{3}{1} = 3\).
- Vì \(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OB'C'\) có:
\(\frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(B'C'//BC\) (định lí Thales đảo)
Vì \(B'C'//BC \Rightarrow \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{BC}}{{B'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{3}{1} = 3\).
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
ii) Xét tam giác \(A'B'C'\) và tam giác \(ABC\) ta có:
\(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (chứng minh trên)
Do đó, tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\).

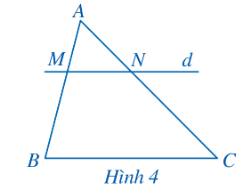
Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

Ta có:
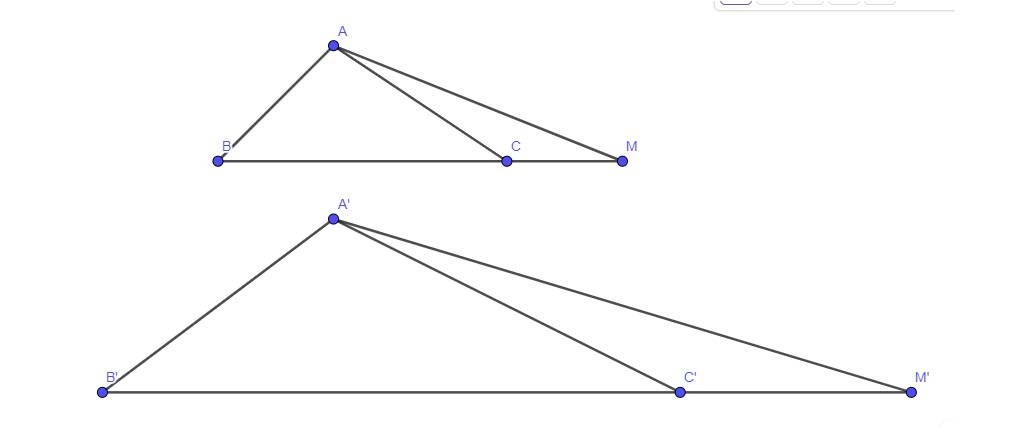
\(\begin{array}{l}\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\\ \Rightarrow \frac{{MB - BC}}{{MB}} = \frac{{M'B' - B'C'}}{{M'B'}}\\ \Rightarrow 1 - \frac{{BC}}{{MB}} = 1 - \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{BC}}{{MB}} = \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{M'B'}}{{MB}} = \frac{{B'C'}}{{BC}}(1)\end{array}\)
Vì ΔA'B'C' ∽ ΔABC suy ra:
\(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}(2)\end{array}\)
Từ (1) và (2) suy ra:
\(\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\)
Xét tam giác ABM và tam giác A”B”M’ có:
\(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\end{array}\)
Suy ra \(\Delta A'B'M' \backsim \Delta ABM\)

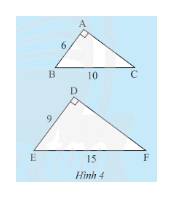
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)

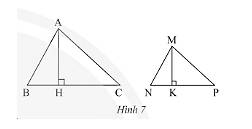
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)

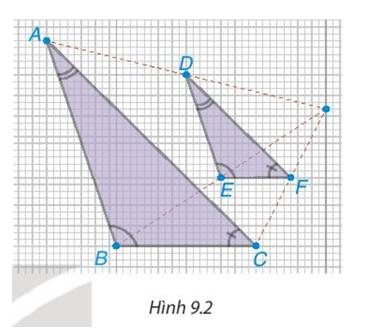
Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)

a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)
hay \(\widehat {HBA} = \widehat {DCB}\)
Xét \(\Delta ABH\) và \(\Delta DCB\) có:
\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)
\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)
b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).
Xét \(\Delta AEB\) và \(\Delta DCB\) có:
\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)
\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)
Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).
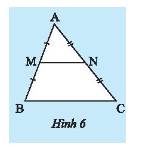



a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))
\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);
Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))
\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).
b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).
c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).
Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).