Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: kết quả của phép tính 5^5 . 5^3 là:
A. 5^15
B. 5^8
C. 25^15
D. 10^8
Câu 2: kết quả của phép tính 3^4 : 3 + 2^3 : 2^2 là:
A. 2
B. 8
C. 11
D. 29
Câu 3: kết quả của phép tính (-13) + (-28) là:
A. -41
B. -31
C. 41
D. -15
Câu4: kết quả của phép tính 5 - (6 - 8) là:
A. -9
B. -7
C.7
D. 3
Câu 5: cho m,n,p,q là những số nguyên. Thế thì m - (n-p + q) bằng:
A. m - n - p + q
B. m-n + p - q
C. m + n - p - q
D. m - n - p - q
Câu 6: cho x - (-9) = 7. Số x bằng:
A. -2
B. 2
C. -16
D. 16


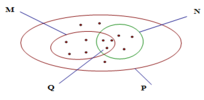
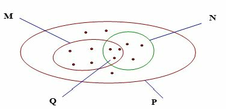
a, Đúng
b, Đúng
c, Sai vì có những phần tử của N không phải là phần tử của M

Đáp án là B
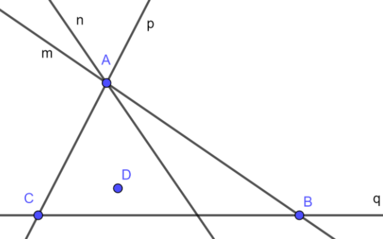
Điểm A thuộc 3 đường thẳng m, n và p ⇒ 1_b
Điểm B thuộc 2 đường thẳng m và q ⇒ 2_d
Điểm C thuộc hai đường thẳng p và q ⇒ 3_e
Điểm D không thuộc các đường thẳng m, n, p và q ⇒ 4_a

a)
Giả sử: m.x = p suy ra n.x = q (phép nhân tử và mẫu cho cùng một số của cấp 1)
VP = \(\dfrac{m+p}{n+q}=\dfrac{m+mx}{n+nx}=\dfrac{m\left(1+x\right)}{n\left(1+x\right)}=\dfrac{m}{n}=\dfrac{p}{q}\)= VT
b)
Tương tự như trên:
VP = \(\dfrac{m-2p}{n-2q}=\dfrac{m-2mx}{n-2nx}=\dfrac{m\left(1-2x\right)}{n\left(1-2x\right)}=\dfrac{m}{n}\) = VT
c)
Mình nghĩ bạn ghi sai đề đó, nếu theo mình thì
Từ a và b đã chứng minh, ta có
\(\dfrac{p}{q}=\dfrac{m}{n}\)<=> \(\dfrac{m+p}{n+q}=\dfrac{m-2p}{n-2q}\) <=> \(\dfrac{m+p}{m-2p}=\dfrac{n+q}{n-2q}\)

D. m-n-p+q
D