Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3A=3+3^2+3^3+...+3^2017+3^2018
=> 3A-A=3^2018-1
=> 2A=3^2018-1
=> 2A+1=3^2018=(3^1009)^2 là số chính phương
=> 2A không là số chính phương

- Cạnh huyền góc nhọn: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia thì 2 tam giác đó bằng nhau.
- Cạnh góc vuông-góc nhọn kề: Nếu cạnh huyền và góc nhọn kề của tam giác vuông này bằng cạnh huyền và góc nhọn kề tương ứng của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Thêm một trường hợp khác nhé: cạnh huyền- cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và cạnh góc vuông tương ứng của tam giác vuông kia thì hai tam giác vông đó bằng nhau.
Học tốt
Định lí :
Trong tam giác vuông, mỗi cạnh góc vuông bằng :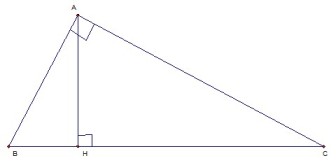
a) Cạnh huyền nhân với sin góc đối hoặc cosin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc cotang góc kề.
Công thức :
AC = BC.sin B = BC.cos C = AB.tg B = AB.cotg C.
AB = BC.sin C = BC.cos B = AC. Tam giác C = AC.cotg B

bài 1:
a)-7129+1478+7129+(-1479)
=(-7129+7129)+(-1479+1479)
= 0 + 0
=0
b)|-5|.(-7)+4.(-9)
=5.(-7)+4.(-9)
=-35+(-36)
=-101
c)1-2+3-4+5-6+...+2009-2010+2011 có tất cả 2011 số
=(1-2)+(3-4)+(5-6)+...+(2009-2010)+2011 có 1005 cặp số
=-1+(-1)+(-1)+...+(-1)+2011
=-1005+2011
=1006
(câu c chị ko chắn là đúng cho lắm,vì thế e nên xem lại nha)
bài 2:
a)x+5=-2+11 b)-3x=-5+29
x+5=9 -3x=24
x=9-5 x=24:(-3)
x=4 x=-8
c)|x|-9=-2+17 d)|x-9|=-2+17
|x|=17+9 |x-9|=15
|x|=26 ⇒ x-9=15 hoặc x-9=-15
⇒x=26 hoặc x=-26 với x-9=15
x=15+9
x=24
với x-9=-15
x=-15+9
x=-6
vậy xϵ{24;-6}
bài 3+4(chị chịu😓😓😓)

Với n = 1 thì 1! = 1 = 1² là số chính phương .
Với n = 2 thì 1! + 2! = 3 không là số chính phương
Với n = 3 thì 1! + 2! + 3! = 1+1.2+1.2.3 = 9 = 3² là số chính phương
Với n ≥ 4 ta có 1! + 2! + 3! + 4! = 1+1.2+1.2.3+1.2.3.4 = 33 còn 5!; 6!; …; n! đều tận cùng bởi 0 do đó 1! + 2! + 3! + … + n! có tận cùng bởi chữ số 3 nên nó không phải là số chính phương .
Vậy có 2 số tự nhiên n thỏa mãn đề bài là n = 1; n = 3.

21 = 7 . 3
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
A= (2+22+23)+...+(258+259+260)
A=2.(1+2+22)+...+258.(1+2+22)
A=2.7+...+258.7
A=7.(2+...+258)
Vì 7 chia hết cho 7 =>7.(2+...+258) chia hết cho 7
=>A chia hết cho 7
Vì A cùng chia hết cho 7 ; 3 đồng nghĩa với A chia hết cho 21 .

đúng nha bạn
người có 13 điểm hỏi đáp trở lên k được 1sp
ctv k được 3sp
giáo viên tích được 6sp
mk nghĩ là ko thể
mik nghĩ là ko thể chứng minh 2=1đc đâu bạn nhé