Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta chọn hệ trục tọa độ sao cho các đỉnh của hình lập phương có tọa độ là:
A(0; 0; 0), B(1;0; 0), D(0; 1; 0)
B’(1; 0 ; 1), D’(0; 1; 1), C’ (1; 1; 1)
d((AB′D′),(BC′D)) = d(A,(BC′D)) = 1/ 3

Chọn hệ trục tọa độ Oxyz sao cho A)0 ; 0 ; 0), B(1 ; 0 ; 0), D(0 ; 1; 0), A'(0 ; 0 ; 1)
Khi đó
B'(1 ; 0 ; 1), D'(0 ; 1 ; 1), C(1 ; 1 ; 0). Phương trình mặt phẳng (A'BD) có dạng:
x + y + z - 1 = 0. (1)
Ta tìm được phương trình mặt phẳng (B'D'C):
Vectơ: (0 ; -1 ; 1) ;
(-1 ; 0 ; 1).
Mặt phẳng (B'D'C) qua điểm C và nhận = (-1 ; -1 ; -1 ) làm vectơ pháp tuyến. Phương trình mặt phẳng (B'D'C) có dạng:
x + y + z - 2 = 0 (2)
Ta có

Mặt phẳng (BC’D) có VTPT 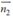 (1;1; -1) và qua B (1; 0;0) nên có phương trình:
(1;1; -1) và qua B (1; 0;0) nên có phương trình:
1( x- 1) + 1( y – 0) - 1( z- 0)= 0 hay x + y - z - 1 = 0
Khoảng cách giữa hai mặt phẳng song song (AB’D’) và (BC’D) chính là khoảng cách từ A đến (BC’D) và bằng :
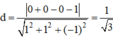



http://123doc.org/document/1883740-phuong-phap-dung-truc-toa-do-trong-bai-hinh-hoc-khong-gian-new.htm
mk k copy đc link b ơi