Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)

a, Trường hợp góc-góc-góc không tồn tại vì 2 tam giác có số đo từng góc bằng nhau thì chưa chắc các cạnh đã bằng nhau
b, Một tam giác không thể có 2 góc vuông vì tổng 2 góc vuông bằng 1800 mà trong tam giác không có góc nào có số đo bằng 00
Hoặc có thể giải thích :
Vì nếu 2 cạnh của 1 tam giác mà cùng vuông góc với cạnh còn lại thì hai cạnh đó song song với nhau (không cắt nhau). Mà nếu trong 1 hình mà có 2 cạnh song song với nhau thì đó không thể là hình tam giác .

a) Trường hợp bằng nhau \(g-g-g\) của 1 t/g không tồn tại vì nếu trong 2 tam giác, độ dài của các cạnh có thể thay đổi, không giống với độ dài của tam giác kia nên không xảy ra t/h đó mà có \(c-g-c;g-c-g;c-c-c\)
b) Một tam giác không thể có 2 góc vuông, vì nếu có 2 góc vuông thì nó sẽ trờ thành hình vuông chứ không phải hình tam giác, thế nên tam giác chỉ được có 1 góc vuông.
Cách diễn đạt không được hay cho lắm nên làm ơn thông cảm.
a) Trường hợp góc-góc-góc không tồn tại vì 2 tam giác có số đo từng góc bằng nhau thì chưa chắc các cạnh đã bằng nhau (ví dụ hình dưới)
A B C A` B` C` A = A` B = B` C = C` ^ ^ ^ ^ ^ ^ AB ≠ A`B` BC ≠ B`C` CA ≠ C`A` Như bạn đã thấy, hai tam giác dưới đây không Bằng nhau
b) Ta biết, tổng của một tam giác là 180o, nếu có 2 cạnh trong một tam giác bằng 90o (góc vuông) thì không thể (vì 90o+90o=180o)

B B B A A A B' B' B' A' A' A' C' C' C' C C C
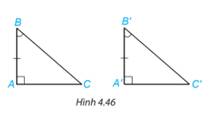
Xét \(\Delta\)ABC và \(\Delta\)A'B'C có :
\(\widehat{A}=\widehat{A'}=90^0\)
AC = A'C'
\(\widehat{B}=\widehat{B'}\)
Ta cần chứng minh \(\Delta\)ABC = \(\Delta\)A'B'C
Ta có : \(\widehat{C}=90^0-\widehat{B},\widehat{C'}=90^0-\widehat{B'}\)
mà \(\widehat{B}=\widehat{B'}\)nên \(\widehat{C}=\widehat{C'}\)
=> \(\Delta\)ABC = \(\Delta\)A'B'C(g.c.g)
Bạn tự vẽ hình nhé!
Tam giác bằng nhau theo TH: cạnh huyền,góc nhọn


Trong hình học Euclid, một tam giác thường được xác định bởi ba cạnh và ba góc. Để một tam giác tồn tại, ta cần biết điều kiện cho ba cạnh và ba góc. Trong trường hợp bạn đề cập, nếu ta có một cạnh là góc vuông và một góc nhọn không kề cạnh với góc vuông đó, thì sẽ xảy ra mâu thuẫn.
Vì trong một tam giác, tổng các góc bằng 180 độ, và trong một tam giác vuông, một góc là 90 độ. Nếu một góc khác không kề với góc vuông, nó sẽ phải nằm ở phần còn lại của tam giác, tức là từ 180 độ trừ đi 90 độ, tức là 90 độ. Nhưng điều này không thể xảy ra vì trong tam giác, không thể có góc nào lớn hơn 90 độ.
Vậy nên, một tam giác với một cạnh là góc vuông và một góc nhọn không kề cạnh với nó không thể tồn tại trong hình học Euclid.