Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử: Lấy a là số kẹo bất kì, b = 0 là số người.
Nếu lấy a chia cho b => a:0
Mà không có người thì chia làm gì
Nên: a : 0 vô lí
Từ đó suy ra được định lí.

Tại công thức không cho bạn nhân như thế.
Làm gì có công thức nào nhân được sin 2x . cos 2x = sin (2x.2) = sin 4x ???
Em phải coi các hàm lượng giác như sin, cos, tan... giống như các hàm kiểu như bình phương hay căn thức.
Có nghĩa là chúng phải (bắt buộc) biến đổi thông qua các công thức lượng giác cơ bản.
Ví dụ: \(\sqrt{2}+\sqrt{3}\) chúng ta không thể tính thành: \(\sqrt{2}+\sqrt{3}=\sqrt{2+3}\) bằng cách "sáng tạo" đặt dấu căn ra làm nhân tử chung?
Thì sin(x), cos(x) cũng hoạt động như vậy (nhưng còn khác biệt nữa). Chúng ta không thể "sáng tạo" \(sin2x.cos2x=sin.cos\left(2x.2x\right)=????\)
Muốn biển đổi lượng giác thì phải thông qua công thức lượng giác và chỉ công thức lượng giác mà thôi. Mọi "sáng tạo" khác đều dẫn đến sai lầm.

Thay ![]() = x ;
= x ; ![]() là y nhé bạn =='.
là y nhé bạn =='.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}x+y=23\\x\cdot y=132\\y-x=1\end{matrix}\right.\left(ĐK:x,y>0\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=23-y\\x\cdot y=132\\y-\left(23-y\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=23-y\\x\cdot y=132\\2y=24\Rightarrow y=12\end{matrix}\right.\)
Thay y = 12 vào hai đẳng thức trên ta được :
\(x+12=23\Rightarrow x=11\) hay \(x\cdot12=132\Rightarrow x=11\)
Vậy \(\left\{{}\begin{matrix}x=11\\y=12\end{matrix}\right.\) hay ![]() \(=11\);
\(=11\); ![]() \(=12\).
\(=12\).

bạn kể rõ ra xem nào,nếu đăng được ảnh chụp cho mk thì càng tốt
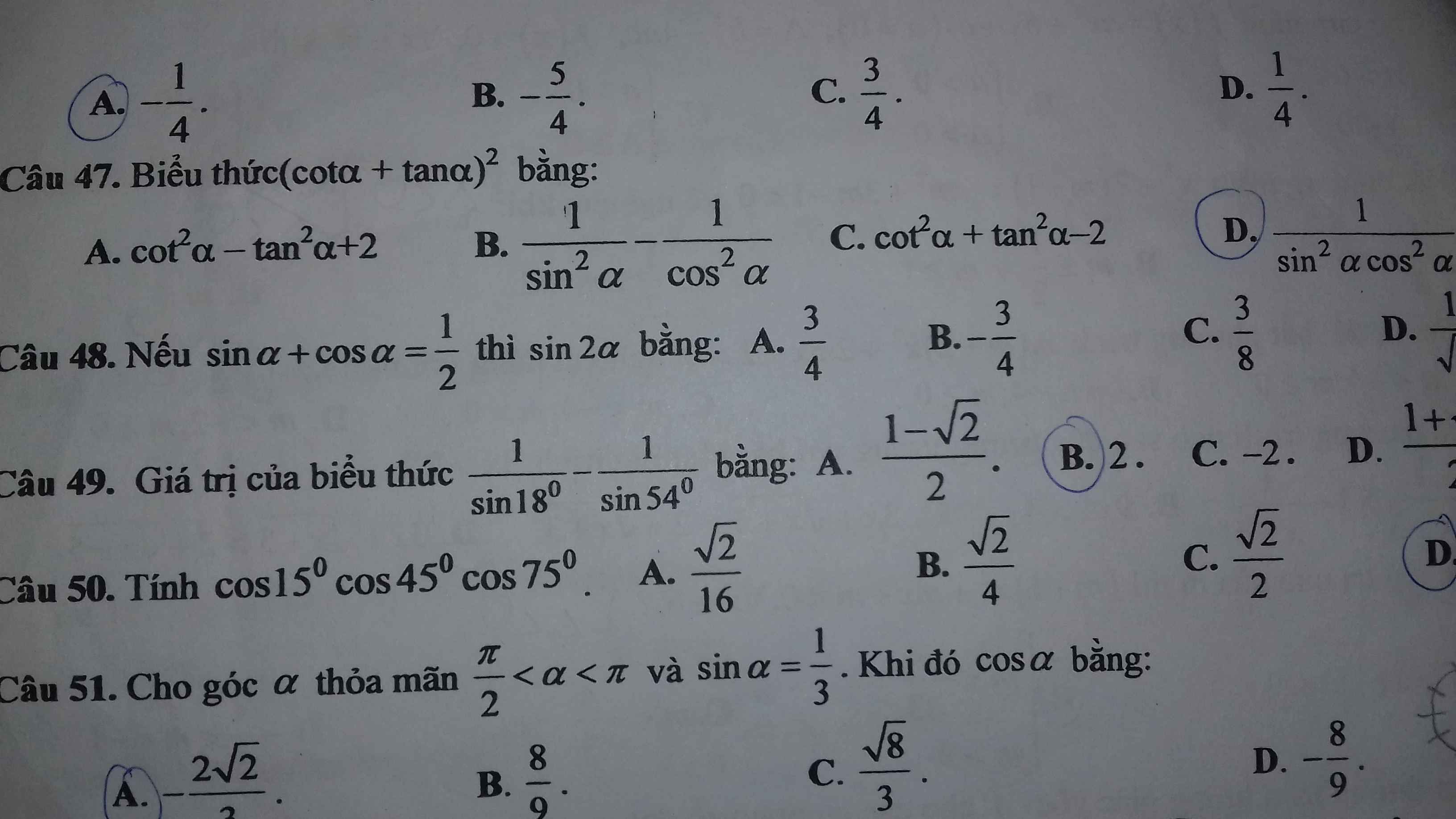







47.
\(\left(cot\alpha+tan\alpha\right)^2=\left(\dfrac{cos\alpha}{sin\alpha}+\dfrac{sin\alpha}{cos\alpha}\right)^2=\left(\dfrac{cos^2\alpha+sin^2\alpha}{sin\alpha.cos\alpha}\right)^2=\dfrac{1}{sin^2\alpha.cos^2\alpha}\)
(cota +tana)\(^2\)=cot\(^2\)a+2cota.tana+tan\(^2\)a=(cot\(^2\)a +1)+(tan\(^2\)+1)=\(\dfrac{1}{sin^2a}\)+\(\dfrac{1}{cos^2a}\)=\(\dfrac{cos^2a+sin^2a}{cos^2a.sin^2a}\)=\(\dfrac{1}{cos^2a.sin^2a}\)