TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HX
2
Y
23 tháng 6 2023
\(A=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}+1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\left(dkxd:a>0,a\ne1\right)\)
\(=\dfrac{\sqrt{a}+1+a-\sqrt{a}}{\left(a-\sqrt{a}\right)\left(\sqrt{a}+1\right)}.\dfrac{\sqrt{a^2}-2\sqrt{a}+1}{\sqrt{a}+1}\)
\(=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}.\dfrac{\left(\sqrt{a}-1\right)}{\sqrt{a}+1}\)
\(=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}+1\right)^2}\)
\(B=\dfrac{3}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\left(dkxd:x\ge0,x\ne1\right)\)
\(=\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{1+\sqrt{x}-3}{\sqrt{x}-1}\)
\(=\dfrac{3\sqrt{x}-3-\left(1+\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}-3-\sqrt{x}-1-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}+1}\)
\(C=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right).\dfrac{\sqrt{x}-2}{\sqrt{x}}\left(dkxd:x>0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}.\sqrt{x}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
23 tháng 6 2023
a: \(A=\dfrac{\sqrt{a}+1+a-\sqrt{a}}{\left(\sqrt{a}+1\right)\cdot\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\)
\(=\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
b: \(B=\dfrac{3\sqrt{x}-3-\sqrt{x}-1-\sqrt{x}+3}{x-1}=\dfrac{\sqrt{x}-1}{x-1}\)
=1/(căn x+1)
c: \(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{x-4}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{1}{\sqrt{x}+2}=\dfrac{2}{\sqrt{x}+2}\)
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
Y
26 tháng 5 2023
Gọi \(x\left(h\right)\) lần lượt là thời gian dự định đi từ Huế đến Hội An của hai bạn Lisa và Jisoo và \(y\left(km/h\right)\) là vận tốc dự định \(\left(x,y>0\right)\)
\(45p=0,75h\)
\(30p=0,5h\)
Nếu Lisa giảm vận tốc 10 km/h thì thời gian để đến Hội An tăng 45 phút : \(\left(y-10\right)\left(x+0,75\right)=xy\)
\(\Leftrightarrow xy+0,75y-10x-7,5=xy\)
\(\Leftrightarrow-10x+0,75y=7,5\left(1\right)\)
Nếu Lisa tăng vận tốc 10 km/h thì thời gian giảm 30 phút :
\(\left(y+10\right)\left(x-0,5\right)=xy\)
\(\Leftrightarrow xy-0,5y+10x-5=xy\)
\(\Leftrightarrow10x-0,5y=5\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) ta có hệ pt : \(\left\{{}\begin{matrix}-10x+0,75y=7,5\\10x-0,5y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=50\end{matrix}\right.\) \(\left(tmdk\right)\)
Vậy thời gian dự định đi từ Huế đến Hội An của hai bạn Lisa và Jisoo là \(3h\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
26 tháng 5 2023
Anh nhìn đề bé quá không rõ mờ nhoè nữa em
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2023
Gọi vận tốc của xe máy là x(km/h) với x>0
Vận tốc của ô tô là: \(x+20\) (km/h)
Quãng đường xe máy đi được sau 1h: \(x\) (km)
Quãng đường còn lại: \(160-x\) (km)
Tổng vận tốc 2 xe: \(x+x+20=2x+20\) (km/h)
Thời gian xe ô tô đi từ B đến C: \(\dfrac{72}{x+20}\)
Do hai xe đi ngược chiều và gặp nhau tại C nên thời gian từ khi ô tô xuất phát đến khi gặp nhau là: \(\dfrac{160-x}{2x+20}\)
Cả 2 khoảng thời gian nói trên đều là thời gian ô tô đi từ B đến C nên ta có pt:
\(\dfrac{72}{x+20}=\dfrac{160-x}{2x+20}\)
\(\Rightarrow72\left(2x+20\right)=\left(160-x\right)\left(x+20\right)\)
\(\Leftrightarrow x^2+4x-1760=0\Rightarrow\left[{}\begin{matrix}x=40\\x=-44\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc của xe máy là 40 km/h, vận tốc ô tô là 60 km/h
Y
22 tháng 6 2023
\(B=\dfrac{2+\sqrt{a}}{\sqrt{a}+1}+\dfrac{2-\sqrt{a}}{\sqrt{a}-1}\left(dkxd:a>0,a\ne1\right)\)
\(=\dfrac{\left(2+\sqrt{a}\right)\left(\sqrt{a}-1\right)+\left(2-\sqrt{a}\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{2\sqrt{a}-2+a-\sqrt{a}+2\sqrt{a}+2-a-\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{2\sqrt{a}-\sqrt{a}+2\sqrt{a}-\sqrt{a}}{\sqrt{a^2}-1}\)
\(=\dfrac{2\sqrt{a}}{a-1}\)
GH
22 tháng 6 2023
\(B=\dfrac{\left(2+\sqrt{a}\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}+\dfrac{\left(2-\sqrt{a}\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\\ =\dfrac{2\sqrt{a}-2+a-\sqrt{a}}{a-1}+\dfrac{2\sqrt{a}+2-a-\sqrt{a}}{a-1}\\ =\dfrac{\sqrt{a}-2+a+\sqrt{a}+2-a}{a-1}=\dfrac{2\sqrt{a}}{a-1}\)
HX
1
TM
1
28 tháng 3 2023
1:góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
2: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
ΔoAC cân tại O
mà OI là trung tuyến
nên OI vuông góc AC
góc BAC=1/2*180=90 độ
góc AHO=góc AIO=góc HAI=90 độ
=>AHOI là hìnhchữ nhật
3:
góc DCA=1/2*sđ cung AC=góc ABC
=>ΔACD đồng dạng vơi ΔCBD
=>CD/BD=AC/BC=2CI/2BO=CI/BO
=>BD/BO=CD/CI
HX
2
GH
22 tháng 6 2023
Với m = 3 thì (d): y = 8x - 7
PTHĐGĐ của (P) và (d): \(x^2-8x+7=0\)
Có: \(a+b+c=1+\left(-8\right)+7=0\)
=> PT có 2 nghiệm phân biệt \(x_1=1;x_2=7\)
\(x_1=1\Rightarrow y_1=x_1^2=1^2=1\\ x_2=7\Rightarrow y_2=x_2^2=7^2=49\)
Tọa độ giao điểm của (P) và (d) là: \(\left(1;1\right);\left(7;49\right)\)
b)
PTHĐGĐ của (P) và (d) là:
\(x^2-2\left(m+1\right)x+3m-2=0\)
\(\Delta'=\left(m+1\right)^2-\left(3m-2\right)=m^2+2m+1-3m+2=m^2-m+3\\ =m^2-m+\dfrac{1}{4}+\dfrac{11}{4}=\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall m\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=3m-2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4=20\\ \Leftrightarrow4m^2+2m+8-20=0\\ \Leftrightarrow4m^2+2m-12=0\\ \Leftrightarrow2m^2+m-6=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-2\left(tm\right)\\m=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
Y
22 tháng 6 2023
Gọi tọa độ của \(\left(P\right),\left(d\right)\) là \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\)
\(a,m=3\)
\(\Rightarrow x^2=2\left(3+1\right)x-3.3+2\)
\(\Rightarrow x^2-8x+7=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Thay \(x=7\) vào \(\left(P\right):y=x^2\Rightarrow y=7^2=49\)
Khi m = 3 thì đường thẳng \(\left(d\right):y=2\left(3+1\right)x-3.3+2=8x-7\)
Thay \(x=1\) vào \(\left(d\right):y=8x-7=8.1-7=1\)
Vậy \(A\left(7;49\right),B\left(1;1\right)\)
\(\Rightarrow y=\left(2m+2\right)x-3m+2\)
\(b,\) Vì \(\left(P\right)\) và \(\left(d\right)\) luôn cắt nhau tại 2 điểm pb A,B \(\forall m\) nên :
\(x^2=2\left(m+1\right)x-3m+2\Leftrightarrow x^2-2\left(m+1\right)x+3m-2\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=3m-2\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=20\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4-20=0\)
\(\Leftrightarrow4m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m=-2\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{2},m=-2\) thì thỏa mãn đề bài.
L
1
14 tháng 8 2023
a: \(=\left|4-3\sqrt{2}\right|=3\sqrt{2}-4\)
b: \(\sqrt{\left(2+\sqrt{5}\right)^2}=\left|\sqrt{5}+2\right|=\sqrt{5}+2\)
c: \(\sqrt{\left(4+\sqrt{2}\right)^2}=\left|4+\sqrt{2}\right|=4+\sqrt{2}\)
d: \(\sqrt{\left(2-\sqrt{3}\right)^2}=\left|2-\sqrt{3}\right|=2-\sqrt{3}\)
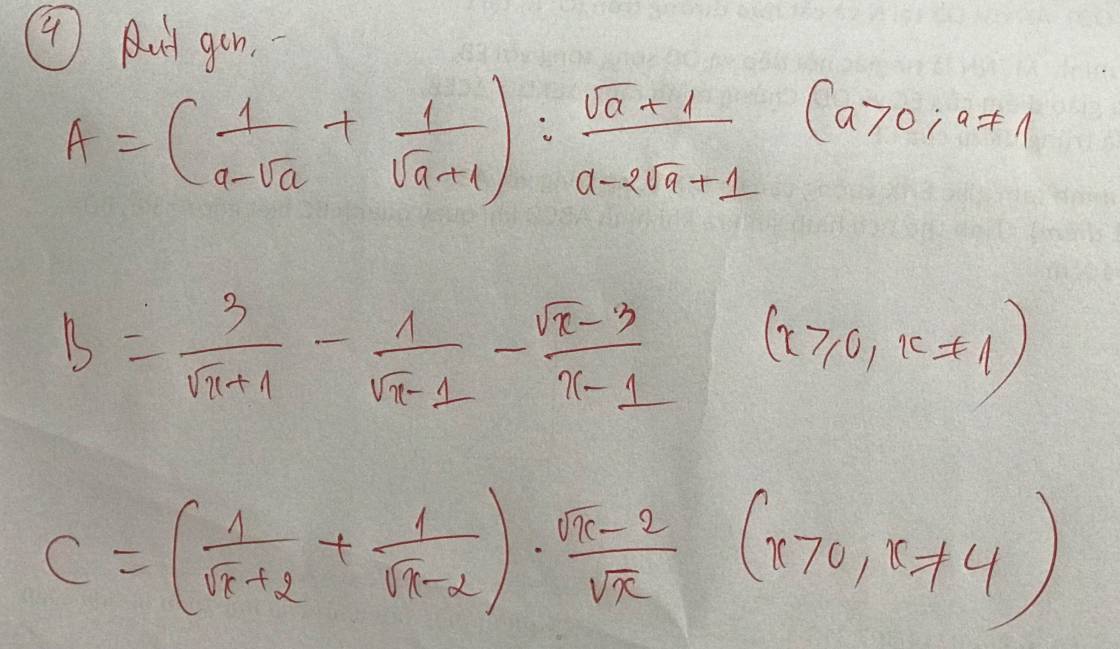
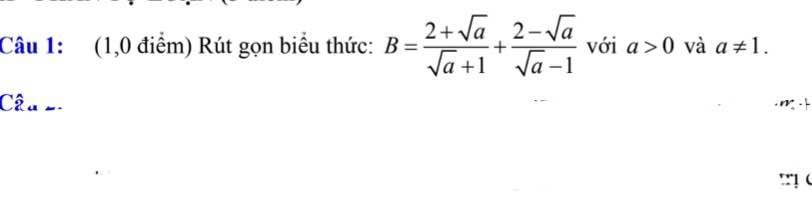
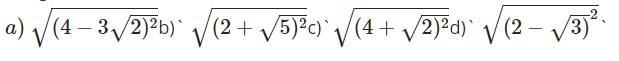
Đề bài đâu bạn?