Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Chuẩn hóa R = 1 => C = 4L
+ Hai giá trị của tần số góc cho cùng hệ số công suất
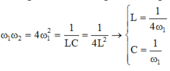
Hệ số công suất của mạch
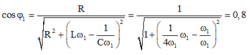

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

Áp dụng CT:
Nếu \(R^2=n\dfrac{L}{C}\)
Thì: \(\cos\varphi = \dfrac{1}{\sqrt{1+\dfrac{1}{n}(\dfrac{\omega_1}{\omega_2}-\dfrac{\omega_2}{\omega_1})^2}}\)
Ta được: \(\cos\varphi = \dfrac{1}{\sqrt{1+\dfrac{1}{1}(\dfrac{50}{200}-\dfrac{200}{50})^2}}=...\)

Chuẩn hóa R + r = 1.
→ Hệ số của suất của mạch
cos φ = 2 13 = 1 1 + ω 1 ω 2 − ω 2 ω 1 2 ⇒ ω 1 ω 2 = 1 4
Từ đó ta tìm được ω 1 = 40 r a d / s .
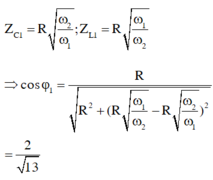
Đáp án A

Từ biểu thức L = C R 2 ⇒ Z L Z C = R 2
Gọi n giá trị của cảm kháng khi tần số của dòng điện là ω 1
Chuẩn hóa R = 1 Z L = n ⇒ Z C = 1 n
Từ giả thuyết của bài toán
cos φ 1 = cos φ 2 ⇔ 1 1 2 + n − 1 n 2 = 1 1 + 4 n − 1 4 n 2 ⇔ n − 1 n = − 4 n − 1 4 n ⇒ n = 1 2
Hệ số công suất của mạch
cos φ 1 = 1 1 2 + n − 1 n 2 = 2 13
Đáp án A

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V
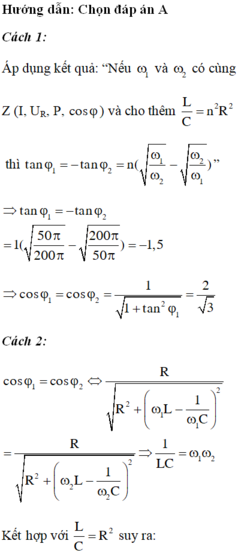

Chuẩn hóa R = 1 ⇒ C = 4 L
Hai giá trị của tần số góc cho cùng hệ số công suất
ω 1 ω 2 = 4 ω 1 2 = 1 L C = 1 4 L 2 ⇒ L 2 = 1 16 ω 1 2
Hệ số công suất của mạch
cos φ = 1 1 + 1 16 ω 1 2 ω 1 − ω 2 2 = 0 , 8
Đáp án D