

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Đáp án A

Ta nhận thấy đồ thị trên thể hiện sự phụ thuộc của cường độ dòng điện I khi thay đổi tần số gốc
Cường độ dòng điện được tính theo biểu thức
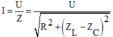
Nên I m a x = U R khi ω = ω 0
Đối với ω = ω 1 ; ω = ω 2 thì I 1 = I 2 = I 5
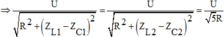
Khi ω 2 > ω 1 thì Z L 2 > Z L 1 ; Z C 2 < Z C 1 nên
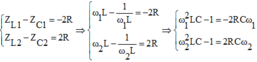
Nên ta có ![]()
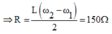

Đáp án A
Khi U R = max ⇒ ω = 1 L C
Khi U L = max ⇒ Z C = L C − R 2 2 ⇔ 1 ω L C = L C − R 2 2
⇒ ω L = 1 L C − R 2 C 2 2 > 1 L C
Khi U C = max ⇒ Z C = L C − R 2 2 ⇔ ω C L = L C − R 2 2
⇒ ω C = 1 L C − R 2 2 L 2 < 1 L C ⇒ ω R 2 = ω L ω C ω C < ω R < ω L
Vậy khi ω thay đổi từ 0 → ∞ thì U C đạt max trước rồi đến U R rồi đến U L
Theo đồ thị ⇒ (1) là U C , (2) là U R và (3) là U L

Chọn đáp án C.
L thay đổi để U C và P max khi mạch xảy ra cộng hưởng
=> Z L 0 = x 1 = Z C
+ Mặt khác khi đó ta có: Z = R
=> I = U R = 1 A
Khi đó:
U C m a x = 80 V ⇒ Z C = 80 1 = 80 Ω ⇒ x 1 = 80 Ω
+ L thay đổi với 2 giá trị Z L = 35 Ω và Z L = x 2 mạch có cùng công suất
⇒ 35 + x 2 = 2 x 1 ⇒ x 2 = 125 Ω
+ Bên cạnh đó khi Z L = x 2 là giá trị của Z L để U L m a x
125 = R 2 + Z C 2 Z C = R 2 + 80 2 80 ⇒ R = 60 Ω