Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thức tổng điện áp cho mạch nối tiếp là:
U = U1 + U2 + U3 + ...
Ở đây, chúng ta có ba điện trở nối tiếp có giá trị lần lượt là R, 2R và 3R. Hiệu điện thế giữa hai đầu của chúng đã được đo là U1 và U2.
U1 = 40,6 V U2 = 72,5 V
Giờ, chúng ta muốn tính hiệu điện thế giữa hai đầu của điện trở 3R. Đặt U3 là hiệu điện thế này.
Sử dụng công thức tổng điện áp, chúng ta có:
U = U1 + U2 + U3
U3 = U - U1 - U2
Đưa giá trị U1 và U2 vào công thức:
U3 = U - 40,6 V - 72,5 V
Giả sử hiệu điện thế U không đổi, nghĩa là U1 + U2 + U3 = U. Chúng ta có thể tìm giá trị của U bằng cách cộng tổng các hiệu điện thế U1, U2 và U3 lại với nhau:
U = U1 + U2 + U3 = 40,6 V + 72,5 V + U3
Giờ, chúng ta cần tìm giá trị của U3:
U3 = U - (40,6 V + 72,5 V)
U3 = U - 113,1 V
Giờ, chúng ta không biết giá trị cụ thể của U, nhưng chúng ta biết rằng nếu chuyển vôn kế đó sang hiệu điện thế giữa hai đầu điện trở 3R thì U3 sẽ bằng 0, vì không có hiệu điện thế nào xuất hiện giữa hai đầu của điện trở 3R.
Vì vậy, ta có phương trình:
0 = U - 113,1 V
Suy ra:
U = 113,1 V
Vậy, khi chuyển vôn kế sang hiệu điện thế giữa hai đầu điện trở 3R, giá trị của vôn kế sẽ là 113,1 V.

Tóm tắt:
\(R_0=6000\Omega\)
\(R_1=2000\Omega\)
\(R_2=4000\Omega\)
\(U_{MN}=60V\)
a) K mở \(U_1=?\) \(U_2=?\)
-------------------------------------
Bài làm:
- Sơ đồ mạch điện:\(\left(R_1ntR_2\right)\text{//}R_0\)
Từ sơ đồ mạch điện: \(\Rightarrow R_{12}=R_1+R_2=2000+4000=6000\Omega\)
Vì \(R_{12}\text{//}R_0\) nên \(U_{MN}=U_{12}=U_0=60V\)
Cường độ dòng điện chạy qua điện trở R12 là:
\(I_{12}=\dfrac{U_{12}}{R_{12}}=\dfrac{60}{6000}=0,01\left(A\right)\)
Vì \(R_1ntR_2\) nên \(I_1=I_2=I_{12}=0,01\left(A\right)\)
Số chỉ của vôn kế 1 là:
\(U_1=I_1\cdot R_1=0,01\cdot2000=20\left(V\right)\)
Số chỉ của vôn kế 2 là:
\(U_2=I_2\cdot R_2=0,01\cdot4000=40\left(V\right)\)
Vậy..........................
a) v1 chi 20v
v2 chi 40v
b)Rac=2000![]()
Rcb=4000
Uv=0v
c)Rac=4000
Rcb=2000
![]()
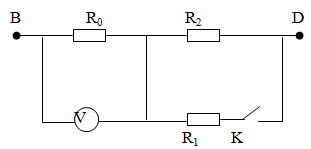
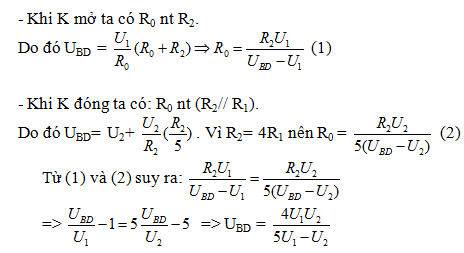

TH1: K mở =>R0 nt R2
\(=>U1=I0.R0\left(V\right)\)
\(=>Ubd=I0.Rtd=\dfrac{U1}{R0}\left(R0+R2\right)=>Ubd=U1+\dfrac{U1.R2}{R0}\)
\(=>\dfrac{U1.R2}{R0}=Ubd-U1=>R0=\dfrac{U1.R2}{Ubd-U1}\)
Th2: R0 nt (R1//R2)
\(=>U0=U2\)
\(=>Ubd=U2+I0.R12=U2+\dfrac{U2}{R0}.\dfrac{R1.R2}{R1+R2}\)
\(=>Ubd=U2+\dfrac{U2}{R0}.\dfrac{\dfrac{R2}{4}.R2}{\dfrac{R2}{4}+R2}=U2+\dfrac{U2}{R0}.\dfrac{\dfrac{R2^2}{4}}{\dfrac{5R2}{4}}\)
\(=U2+\dfrac{U2}{R0}.\dfrac{R2}{5}=>Ubd=U2+\dfrac{U2.R2}{5R0}\)
\(=>R0=\dfrac{U2.R2}{5\left(Ubd-U2\right)}\)
\(=>\dfrac{U1.R2}{Ubd-U1}=\dfrac{U2.R2}{5\left(Ubd-U2\right)}\)
\(=>Ubd=\dfrac{4U1U2}{5U1-U2}\)