Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Biểu diễn vecto các điện áp:
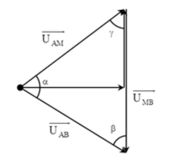
- Áp dụng định lý sin trong tam giác, ta có:
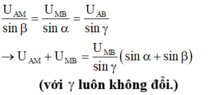
⇒ Biến đổi lượng giác:
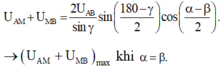
- Khi đó:
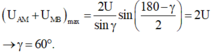
→ Các vecto hợp với nhau thành tam giác đều → khi xảy ra cực đại u chậm pha hơn i một góc 30°.
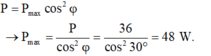


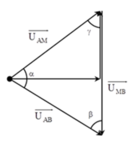
Các vecto hợp với nhau thành tam giác đều => khi xảy ra cực đại u chậm pha hơn i một góc 30 o .
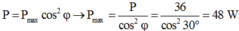

Đáp án D
Phương pháp: Áp dụng phương pháp giản đồ vectơ trong mạch điện xoay chiều
Cách giải:
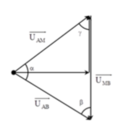
+ Biểu diễn vecto các điện áp.
+ Áp dụng định lý sin trong tam giác
ta có U A M sin β = U M B sin α = U A B sin γ → U A M + U M B = U M B sin γ ( sin α + sin β ) với γ luôn không đổi.
Biến đổi lượng giác U A M + U M B = 2 U A B sin γ sin 180 - γ 2 cos α - β 2 khi α = β .
+ Khi đó U A M + U M B m a x = 2 U sin γ sin 180 - γ 2 = 2 U → γ = 60 0
Các vecto hợp với nhau thành tam giác đều => khi xảy ra cực đại u chậm pha hơn i một góc 30 độ.
P = P m a x cos 2 φ → P m a x = P cos 2 φ = 48 W

Đặt \(Z_L = x, Z_c = y\)
Công suất: \(P = R.I^2 = \frac{RU^2}{R^2 + (x - y)^2} = 210 W\)
Mặt khác: \(f(x) = U_{RC} + U_L = (Z_{RC} + Z_L)I = \frac{U(\sqrt{R^2 + y^2} + x)}{\sqrt{R^2 + x^2 + y^2 - 2xy}}\)
Lấy đạo hàm f(x) và cho \(f'(x) = 0\) suy ra \(x = \sqrt{R^2 + y^2}\)
Khi đó \(f_{max} = 2\sqrt{2}U\) nên suy ra \(y = \frac{3}{4}\sqrt{R^2 + y^2} \Rightarrow y = \frac{3R}{\sqrt{7}}\Rightarrow x = \frac{4R}{\sqrt{7}}\)
\(\Rightarrow \frac{RU^2}{R^2 + (\frac{4R}{\sqrt{7}} - \frac{3R}{\sqrt{7}})^2} = 210 W \Leftrightarrow \frac{7U^2}{8R} = 210 \Rightarrow P_{max} = \frac{U^2}{R} = 240 W\)

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

Lúc sau: \(P'=\frac{U^2.R^2}{R^2_2+Z^2_C}=\frac{U^2.R^2}{R^2_2+R_1R_2}=\frac{U^2}{R_1+R_2}=P=85W\)
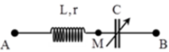
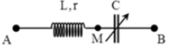
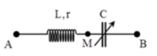
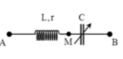
Chọn đáp án D