Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Hiệu điện thế ở 2 đầu đoạn mạch là
\(U=R_1I_1=12.0,2=2,4\) (V)
b. Dòng điện đi qua \(R_2\) và \(R_3\) lần lượt là
\(I_2=\dfrac{U}{R_2}=0,24\) (A)
\(I_3=\dfrac{U}{R_3}=0,16\) (A)
Điện trở tương đương của mạch là
\(\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}\Rightarrow R=4\left(\Omega\right)\)
Cường độ dòng điện qua mạch chính là
\(I=\dfrac{U}{R}=0,6\) (A)
Chúc em học tốt.

a)
Điện trở tương đương của điện trở 2 và 3:
Vì R2//R3 nên R23= \(\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{15.10}{15+10}=6\Omega\)
Điện trở tương đương toàn mạch:
Vì R1 nt R23 nên \(R_{tđ}=R_1+R_{23}=30+6=36\Omega\)
b)
Cường độ dòng điện mạch chính:
\(I=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{24}{36}=\dfrac{2}{3}\)A
Cường độ dòng điện chạy qua điện trở R1:
Vì R1 nt R23 nên I1= I23 = I = \(\dfrac{2}{3}\)A
Hiệu điện thế giữa hai đầu điện trở R1:
I1= \(\dfrac{U_1}{R_1}=>U_1=R_1.I_1=30.\dfrac{2}{3}=20V\)
Hiệu điện thế giữa hai đầu điện trở R2 và R3:
Vì R1 nt R23 nên U1 + U23 = U
=> U23= U - U1 = 24 - 20 = 4V
Hiệu điện thế giữa hai đầu điện trở R2:
Vì R2 // R3 nên U2 = U3 = U23 = 4V
Cường độ dòng điện giữa hai đầu điện trở R2:
\(I_2=\dfrac{U_2}{R_2}=\dfrac{4}{15}A\)
Cường độ dòng điện giữa hai đầu điện trở R3:
\(I_3=\dfrac{U_3}{R_3}=\dfrac{4}{10}=\dfrac{2}{5}A\)
c)
Công của dòng điện sinh ra trong 5 phút:
\(A=\dfrac{U^2}{R^{ }}t=\dfrac{24^2}{36}.300=4800\left(J\right)\)
Tóm tắt :
Biết : \(R_1=30\Omega\) ; \(R_2=15\Omega\) ; \(R_3=10\Omega\)
\(U_{AB}=24V\)
\(t=5'=300s\)
Tính : a. \(R_{AB}\)
b. \(I_1=?\) ; \(I_2=?\) ; \(I_3=?\)
c. \(A=?\)
Giải
a. Ta có \(R_2\)//\(R_3\) nên :
\(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{15.10}{15+10}=6\Omega\)
Vì \(R_1\) nt \(R_{23}\) nên điện trở tương đương toàn mạch là :
\(R_{AB}=R_1+R_{23}=30+6=36\Omega\)
b. \(R_1\) nt \(R_{23}\) nên :
\(I_1=I_{23}=I_{AB}=\dfrac{U_{AB}}{R_{AB}}=\dfrac{24}{36}=\dfrac{2}{3}A\)
\(\Rightarrow U_{23}=I_{23}.R_{23}=\dfrac{2}{3}.6=4V\)
\(\Rightarrow U_2=U_3=4V\) (do \(R_2\) // \(R_3\))
CĐDĐ qua mỗi điện trở là :
\(I_2=\dfrac{U_2}{R_2}=\dfrac{4}{15}A\)
\(I_3=\dfrac{4}{10}=0,4A\)
c. Công của dòng điện sinh ra trong đoạn mạch AB trong 5' là :
\(A=P.t=U.I.t=24.\dfrac{2}{3}.300=4800J\)
Đáp số : a. \(R_{AB}=36\Omega\)
b. \(I_1=\dfrac{2}{3}A\) ; \(I_2=\dfrac{4}{15}A\) ; \(I_3=0,4A\)
c. \(A=4800J\)

Điện trở tương đương: \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(15+25\right)10}{15+25+10}=8\Omega\)
\(U=U12=U3=12V\)(R12//R3)
\(I=U:R=12:8=1,5A\)
\(I3=U3:R3=12:10=1,2A\)
\(R1ntR2\Rightarrow I12=I1=I2\)
Mà: \(I12=I-I3=1,5-1,2=0,3A\)
\(\Rightarrow I12=I1=I2=0,3A\)

Ta thấy I1 = I23= 0,4A
Điện trở tương đương của đoạn mạch AB là:
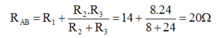
Hiệu điện thế của mạch là:
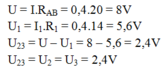
Cường độ dòng điện qua điện trở R2: 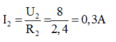
Cường độ dòng điện qua điện trở R3: 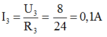
→ Đáp án D

R 2 mắc song song với R 3 nên U 23 = U 2 = U 3
↔ I 2 . R 2 = I 3 . R 3 ↔ I 2 .8 = I 3 .24 ↔ I 2 = 3 I 3 (1)
Do R 1 nt R 23 nên I = I 1 = I 23 = 0,4A = I 2 + I 3 (2)
Mà R 2 // R 3 nên I 2 + I 3 = I 23 = 0,4A (2)
Từ (1) và (2) → I 3 = 0,1A; I 2 = 0,3A

Hiệu điện thế giữa hai đầu R 3 : U 3 = I 3 . R 3 = 0,3.10 = 3V.
⇒ U 23 = U 2 = U 3 = 3V (vì R 2 // R 3 ).
Cường độ dòng điện qua R 2 : I 2 = U 2 / R 2 = 3/15 = 0,2A.
Cường độ dòng điện qua R 1 : I = I 1 = I 2 + I 3 = 0,3 + 0,2 = 0,5A (vì R 1 nằm ở nhánh chính, R 2 và R 3 nằm ở hai nhánh rẽ)

Điện trở tương đương của R2 và R3 là:
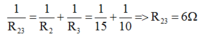
Hiệu điện thế giữa hai đầu R3 là:
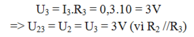
Cường độ dòng điện qua R2 là:
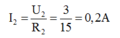
Cường độ dòng điện qua R1 là:
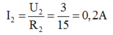
Cường độ dòng điện qua R1 là: I 1 = I = I 2 + I 3 = 0 , 5 A
Hiệu điện thế giữa hai đầu đoạn mạch AB là:
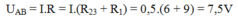
→ Đáp án C
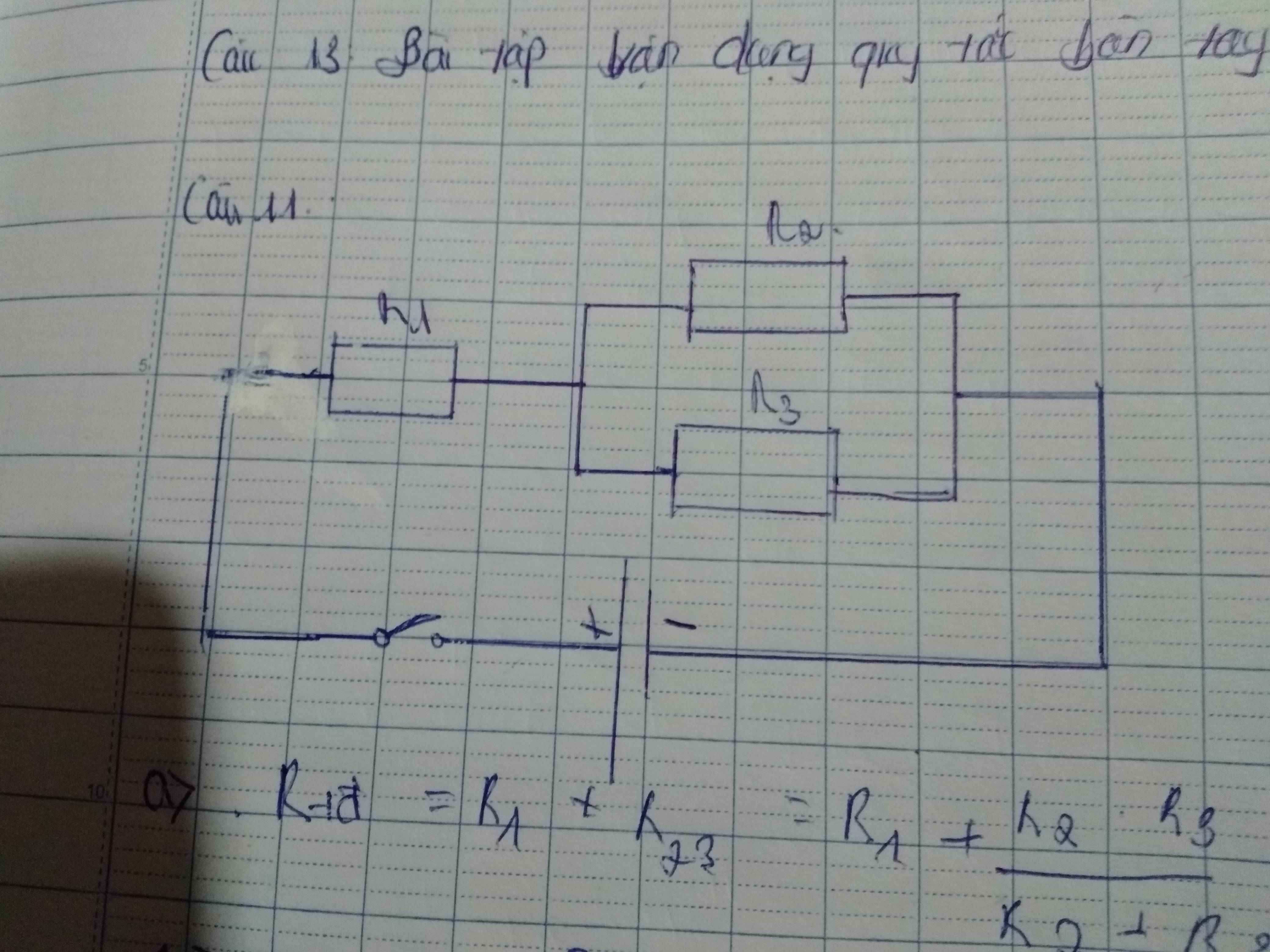 đdđ đi qua mỗi điện trở
đdđ đi qua mỗi điện trở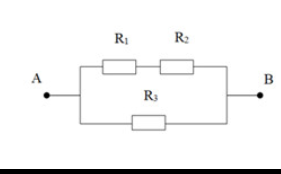
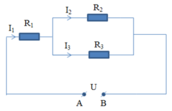
\(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{15.20}{15+20}=\dfrac{60}{7}\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=10+\dfrac{60}{7}=\dfrac{130}{7}\left(\Omega\right)\)
\(U_{23}=U_2=U_3=I_3.R_3=0,1.20=2\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{2}{15}\left(A\right)\)
\(I=I_1=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{2}{\dfrac{60}{7}}=\dfrac{7}{30}\left(A\right)\)