Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,\(R1nt\left(R2//R3\right)=>Rtd=R1+\dfrac{R2R3}{R2+R3}=4+\dfrac{6.3}{6+3}=6\left(om\right)\)
b,\(=>I1=I23=\dfrac{Uab}{Rtd}=\dfrac{9}{6}=1,5A\)
\(=>U23=I23.R23=1,5.\dfrac{6.3}{6+3}=3V=U2=U3\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{3}{6}=0,5A,=>I3=\dfrac{U3}{R3}=\dfrac{3}{3}=1A\)
c,\(=>Im=Ix=I23=\dfrac{1}{3}.1,5=0,5A\)
\(=>RTd=Rx+\dfrac{R2.R3}{R2+R3}=Rx+\dfrac{6.3}{6+3}=\dfrac{U}{Im}=\dfrac{9}{0,5}=18\)
\(=>Rx=16\left(om\right)\)

\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)

Điện trở tương đương: \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(15+25\right)10}{15+25+10}=8\Omega\)
\(U=U12=U3=12V\)(R12//R3)
\(I=U:R=12:8=1,5A\)
\(I3=U3:R3=12:10=1,2A\)
\(R1ntR2\Rightarrow I12=I1=I2\)
Mà: \(I12=I-I3=1,5-1,2=0,3A\)
\(\Rightarrow I12=I1=I2=0,3A\)

a,(ban tu ve hinh)
b,\(\Rightarrow Rtd=\dfrac{R3\left(R1+R2\right)}{R3+R1+R2}=15\Omega\)
c,\(\Rightarrow Im=\dfrac{Um}{RTd}=\dfrac{45}{15}=3A\)
\(\Rightarrow I12=\dfrac{Um}{R1+R2}=\dfrac{45}{30}=1,5A=I1=I2\)
\(\Rightarrow\left\{{}\begin{matrix}U1=I1R1=21V\\U2=I2.R2=24V\end{matrix}\right.\)

a. Vì \(R_1ntR_2\) nên \(R_{12}=R_1+R_2=15+25=40\left(\text{Ω}\right)\)
Vì \(R_{12}//R_3\) nên \(\dfrac{1}{R_{td}}=\dfrac{1}{R_{12}}+\dfrac{1}{R_3}\Rightarrow R_{td}=\dfrac{R_{12}.R_3}{R_{12}+R_3}=\dfrac{40.10}{40+10}=8\left(\text{Ω}\right)\)
b. Ta có \(I=\dfrac{U}{R_{td}}=\dfrac{12}{8}=1,5\left(A\right)\)
mà \(U_{12}=U_3\Leftrightarrow R_{12}.I_{12}=R_3.I_3\Leftrightarrow40I_{12}=10I_3\Leftrightarrow I_3=4I_{12}\) (1)
mặt khác, ta có \(I=I_{12}+I_3\) (2)
Từ (1) và (2) \(\Rightarrow I_{12}+4I_{12}=1,5\Rightarrow I_{12}=0,3\left(A\right)\)
\(\Rightarrow I_3=I-I_{12}=1,5-0,3=1,2\left(A\right)\)
c. Ta có \(R_{td'}=\dfrac{R_{2x}.R_3}{R_{2x}+R_3}=\dfrac{\left(25+R_x\right)10}{R_x+25+10}=\dfrac{250+10R_x}{35+R_x}=7,5\left(\text{Ω}\right)\)
\(\Rightarrow R_x=5\left(\text{Ω}\right)\)
Bạn chụp thêm hình vẽ nữa chứ không biết mắc song song hay nối tiếp để làm

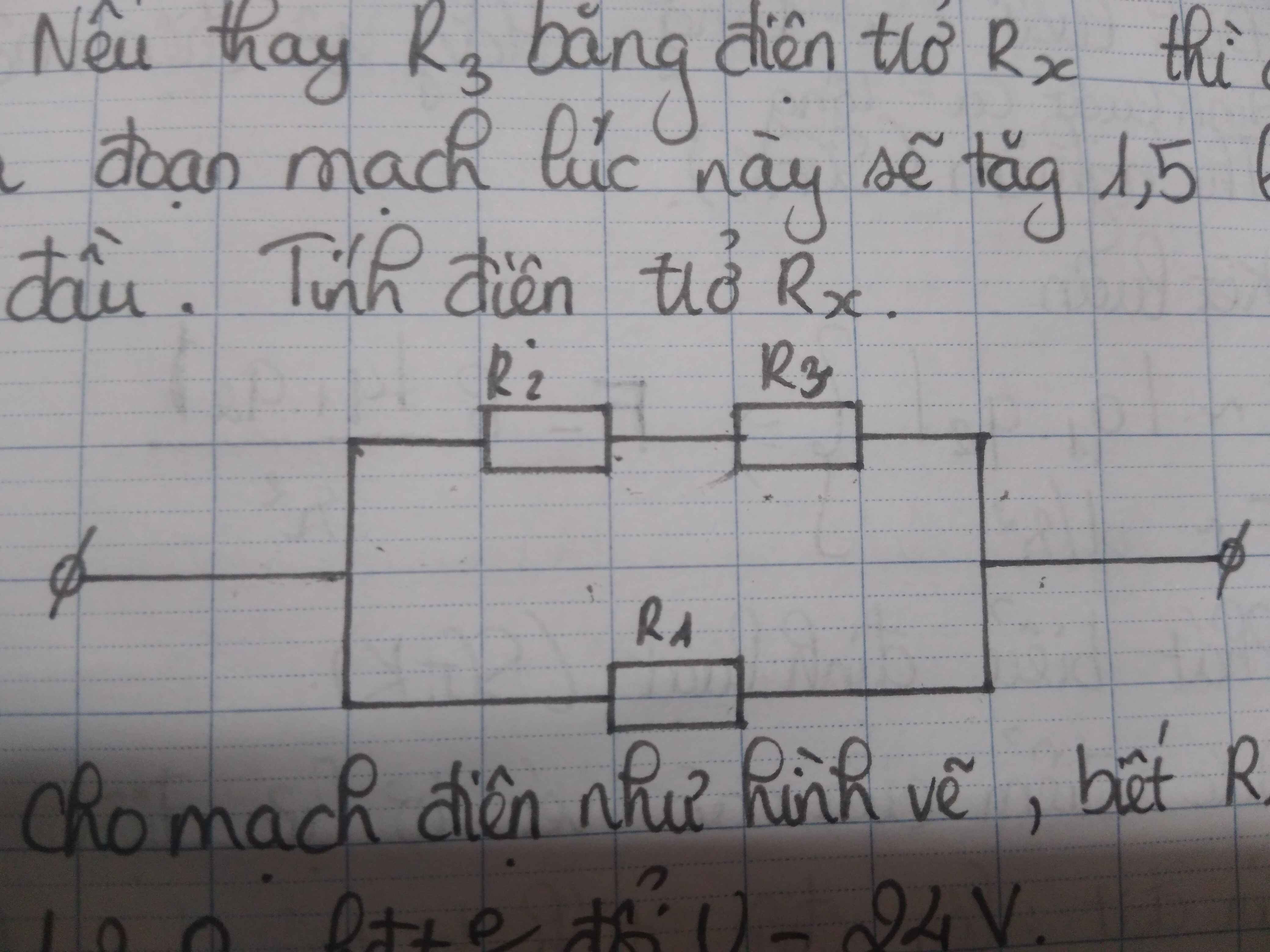
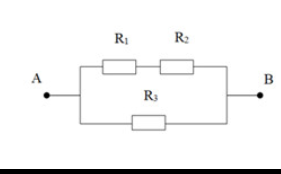
(R1 nt R2)//(R3 nt Rx)
a,\(=>Rtd=\dfrac{\left(R1+R2\right)\left(R3+Rx\right)}{R1+R2+R3+Rx}=\dfrac{\left(12+8\right)\left(16+14\right)}{12+8+16+14}=12\Omega\)
\(=>Im=\dfrac{Um}{Rtd}=\dfrac{48}{12}=4A\)
b, \(=>Ix=Ix3,,,I1=I12\)(gọi điện trở Rx là y(ôm)
theo bài ra \(=>Ix=\dfrac{1}{3}I1=>I3x=\dfrac{1}{3}I12=>I12=3I1x\)
\(=>\dfrac{U12}{R1+R2}=3.\dfrac{U3x}{R3+y}=>\dfrac{48}{12+8}=\dfrac{3.48}{16+y}=>y=44\Omega=>Rx=44\Omega\)