Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
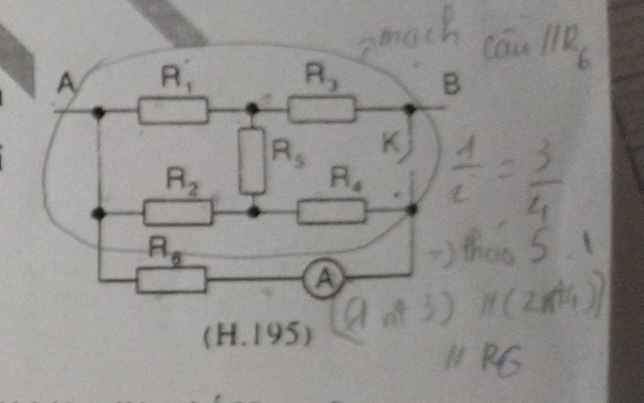
ta thấy \(\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}=2\) => mạch cầu cân bằng => I5=0 U5=0
khi K đóng \(R_{1234}=\dfrac{\left(R_1+R_3\right)\left(R_2+R_4\right)}{R_1+R_2+R_3+R_4}=4\left(\Omega\right)\)
\(R_{td}=\dfrac{R_6.R_{1234}}{R_6+R_{1234}}\)
\(\Rightarrow I_A=I=\dfrac{U_{AB}}{R_{td}}=\dfrac{48}{2}=24\left(A\right)\)
em đang ôn hsg lí 9 à :???
a,\(Rtd=R1+\dfrac{R2R3}{R2+R3}=7+\dfrac{4.12}{4+12}=10\left(om\right)\)
b,\(=>Ia=I1=\dfrac{U}{Rtd}=\dfrac{15}{10}=1,5A\)
c,\(R1nt\left(R2//R3\right)\)
\(=>I1=I23=I2+I3\)
\(=>I1=I2+I3=2A=Im=>U=Im.Rtd=20V\)
vây,,,,,
a)Khóa \(K_1\) đóng, khóa \(K_2\) mở ta có CTM: \(\left(R_1ntR_2\right)//R_3\)
\(I_A=I_m=1A\)
\(R_{12}=R_1+R_2=5+5=10\Omega\)
\(R_{tđ}=\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}=\dfrac{10\cdot15}{10+15}=6\Omega\)
\(U=R_{tđ}\cdot I=6\cdot1=6V=U_{12}=U_3\)
\(I_1=I_2=I_{12}=\dfrac{U_{12}}{R_{12}}=\dfrac{6}{10}=0,6A\)
\(I_3=1-0,6=0,4A\)
b)Khóa \(K_1\) mở và khóa \(K_2\) đóng ta có CTM: \(R_2//\left(R_1ntR_3\right)\)
\(R_{13}=R_1+R_3=5+15=20\Omega\)
\(R_{tđ}=\dfrac{R_2\cdot R_{13}}{R_2+R_{13}}=\dfrac{5\cdot20}{5+20}=4\Omega\)
\(I_A=\dfrac{U}{R_{tđ}}=\dfrac{6}{4}=1,5A\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{U}{R_2}=\dfrac{6}{15}=0,4A\)
\(I_1=I_3=I_{13}=I-I_2=1,5-0,4=1,1A\)
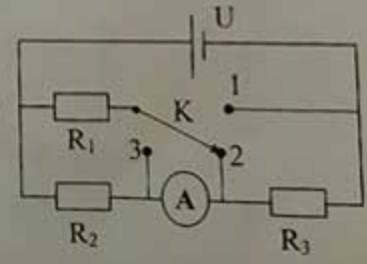
TH1: khoá K ở vị trí 1
\(R_{tđ}=\dfrac{R_1\left(R_2+R_3\right)}{R_1+R_2+R_3}\left(\text{Ω}\right)\)
\(I=\dfrac{U}{R_{tđ}}=\dfrac{U\left(R_1+R_2+R_3\right)}{R_1\left(R_2+R_3\right)}\left(A\right)\)
\(I_{A1}=\dfrac{R_1}{R_1+R_2+R_3}.I=\dfrac{R_1}{R_1+R_2+R_3}.\dfrac{U\left(R_1+R_2+R_3\right)}{R_1\left(R_2+R_3\right)}=\dfrac{U}{R_2+R_3}\left(A\right)\)
Các trường hợp còn lại làm tương tự, ta có
TH2: vị trí khoá K ở 2
\(I_{A2}=\dfrac{UR_1}{R_1R_2+R_2R_3+R_3R_1}\left(A\right)\)
TH3: vị trí khoá K ở 3
\(I_{A3}=\dfrac{U\left(R_1+R_2\right)}{R_1R_2+R_2R_3+R_3R_1}\left(A\right)\)
Ta thấy \(I_{A3}>I_{A2}\left(R_1+R_2>R_1\right)\)
Xét \(I_{A2}-I_{A1}=\dfrac{UR_1}{R_1R_2+R_2R_3+R_3R_1}-\dfrac{U}{R_2+R_3}=\dfrac{-UR_2R_3}{\left(R_2+R_3\right)\left(R_1R_2+R_2R_3+R_3R_1\right)}< 0\Rightarrow I_{A2}< I_{A1}\)
Xét \(I_{A3}-I_{A1}=\dfrac{U\left(R_1+R_2\right)}{R_1R_2+R_2R_3+R_3R_1}-\dfrac{U}{R_2+R_3}=\dfrac{UR_2^2}{\left(R_2+R_3\right)\left(R_1R_2+R_2R_3+R_3R_1\right)}>0\Rightarrow I_{A3}>I_{A1}\)
\(\Rightarrow I_{A3}>I_{A1}>I_{A2}\Rightarrow\left\{{}\begin{matrix}I_{A3}=11mA\\I_{A1}=9mA\\I_{A2}=6mA\end{matrix}\right.\)
b,xét \(\dfrac{I_{A3}}{I_{A2}}=\dfrac{R_1+R_2}{R_1}=\dfrac{11}{6}\Leftrightarrow5R_1=6R_2\Leftrightarrow R_2=\dfrac{5}{6}.2019=\dfrac{2265}{2}\left(\text{Ω}\right)\)
Xét \(\dfrac{I_{A1}}{I_{A2}}=\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_1R_2+R_3R_1}=\dfrac{9}{6}\Rightarrow R_3=\dfrac{R_1R_2}{2R_2-R_1}=\dfrac{10095}{4}\left(\text{Ω}\right)\)