Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_1//R_2\Rightarrow R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{4\cdot6}{4+6}=2,4\Omega\)
Cường độ dòng điện qua mạch chính:
\(I=\dfrac{\xi}{R+r}=\dfrac{12}{2,4+2}=\dfrac{30}{11}A\)
\(U_{AB}=\dfrac{30}{11}\cdot2,4=\dfrac{72}{11}V\Rightarrow U_1=\dfrac{72}{11}V\)
\(\Rightarrow I_1=\dfrac{72}{11}:4=\dfrac{18}{11}A\)

Đáp án: A
Ta có:
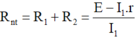
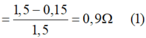
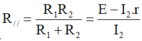
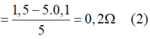
Từ (1) và (2) ⇒ R 1 R 2 = 1 , 8 Ω (3)
Từ (1) và (3)
⇒ R 1 = 0 , 3 Ω ; R 2 = 0 , 6 Ω h o ặ c R 1 = 0 , 6 Ω ; R 2 = 0 , 3 Ω

Áp dụng định luật Ôm dưới dạng U N = IR = E - Ir ta được hai phương trình :
2 = E – 0,5r (1)
2,5 = E – 0,25r (2)
Giải hệ hai phương trình này ta tìm được suất điện động và điện trở trong của nguồn điện là
E = 3V; r = 2 Ω

Ta có: R 23 = R 2 + R 3 = 6 Ω ⇒ R A B = R 1 . R 23 R 1 + R 23 = 2 Ω
Tổng trở của mạch ngoài: R n g = R A B + R 4 = 8 Ω
Cường độ dòng điện trong mạch chính: I = E R n g + r = 1 ( A ) ⇒ I 4 = 1 ( A )
Chọn A

a) Điện trở tương đương mạch ngoài:
\(R_N=R_1+R_2=2+6=8\Omega\)
Cường độ dòng điện qua mạch chính:
\(I_1=I_2=I_m=\dfrac{\xi}{r+R_N}=\dfrac{6}{2+8}=0,6A\)
b) Nhiệt lượng tỏa ra trên điện trở R1 trong \(t=1h20'=4800s\) là: \(Q=R_1I^2t=2\cdot0,6^2\cdot4800=3456J\)
c) Hiệu suất nguồn điện:
\(H=\dfrac{R_N}{R_N+r}=\dfrac{8}{2+8}=0,8=80\%\)




TK:
Để giải bài toán này, ta có thể sử dụng định luật Ohm và định luật Kirchhoff.
1. **Định luật Ohm:** Định luật này nói rằng mối quan hệ giữa điện áp (\(V\)), dòng điện (\(I\)), và điện trở (\(R\)) trong mạch điện là \(V = IR\).
2. **Định luật Kirchhoff:**
- **Định luật tổng điện áp (Định luật thế):** Tổng điện áp trong một vòng dây đóng vai trò tổng điện áp giảm đi qua các điểm của mạch là 0.
- **Định luật tổng dòng điện (Định luật dòng):** Tổng dòng điện đi vào một nút (điểm kết nối) trong mạch bằng tổng dòng điện ra khỏi nút đó.
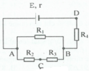
Ta có một mạch điện gồm một nguồn điện có suất điện động \(E\) và một điện trở trong \(r\) nối tiếp, sau đó mạch ngoài có hai điện trở \(R_1 = 40 \Omega\) và \(R_2 = 120 \Omega\) mắc song song.
Gọi \(I\) là cường độ dòng điện trong mạch. Ta biết rằng \(I_1 = 0.25 \text{ A}\) là cường độ dòng điện qua \(R_1\).
Đầu tiên, ta cần tìm suất điện động của nguồn \(E\). Áp dụng định luật tổng điện áp (Định luật thế), tổng điện áp giảm qua mạch là \(0\). Vậy:
\[E = IR + IR_1 = I(r + R_1)\]
\[E = I(2 + 40) = 42I\]
Tiếp theo, ta cần tìm cường độ dòng điện qua \(R_2\). Vì \(R_1\) và \(R_2\) mắc song song, nên tổng điện áp giảm qua \(R_1\) và \(R_2\) là \(E\). Sử dụng định luật Ohm cho \(R_2\), ta có:
\[E = IR_2\]
\[I = \frac{E}{R_2} = \frac{42I}{120}\]
\[I = \frac{7}{20} \text{ A} = 0.35 \text{ A}\]
Vậy, suất điện động của nguồn là \(E = 42 \text{ V}\) và cường độ dòng điện qua \(R_2\) là \(0.35 \text{ A}\).