Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

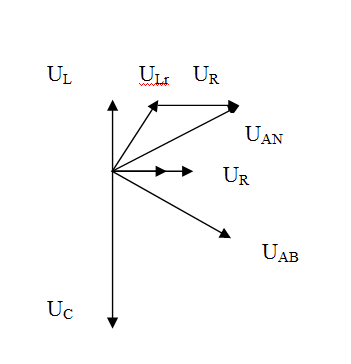
Ta có: \(U_{AB}=U_{AN}=\sqrt{3}U_{MN}=120V\) \(U_R=120V\) \(U_{AB}=U_{AN}\) do đó \(Z_L=U_{LC}\) hay góc hợp giữa \(U_{AB}\) và I bằng góc hợp bởi \(U_{AN}\) và I (cùng có R và r) Mặt khác theo đầu bài của các góc bằng nhau ta suy ra được \(\overrightarrow{U_{AN}}\) là phân giác của góc hợp bởi \(U_{Lr}\) và I \(\overrightarrow{U_{AN}}=\overrightarrow{U_{Lr}}+\overrightarrow{U_R}\) Xét tam giác đã tịnh tiến \(\overrightarrow{U_R}\) lên trên thì theo góc so le của 2 đường song song suy ra đây là tam giác cân \(U_{Lr}=U_R=120V\) Từ đó suy ra góc nhỏ trong tam giác bằng \(\pi\text{ /}6\) Do đó \(U_L=60\sqrt{3}V\) \(Z_L=\frac{U_L}{I}=15\sqrt{6}\Omega\)
|

Với các bài trắc nghiệm khi thi đại học lý cũng như hóa có một số bài dạng này, bạn nhận xét giá trị của hiệu điện thế không ảnh hưởng đến kết quả nên bạn có thể 1 giá trị cụ thể cho hiệu điện thế.
Như bài này mình sẽ lấy hiệu điện thế hiệu dụng là 12V
Dẫn đến tính được R,Zl,Zc lần lượt là \(3\Omega;2\Omega;6\Omega\)
Khi mắc cả vào mạch thì \(z=5\Omega\)
Cường độ dòng sẽ là 2,4 A

Mạch chỉ gồm tụ điện và điện trở nên
\(U_C=U_{AB}.\sin\alpha=50\sqrt{3}V\)
đáp án A

\(\varphi=\varphi_u-\varphi_i=0-\left(-\frac{\pi}{4}\right)=\frac{\pi}{4}\)
\(\tan\varphi=\frac{Z_L-Z_C}{R}=1\Rightarrow Z_L-Z_C=R\)
\(\Rightarrow Z=\sqrt{R^2+\left(Z_L-Z_C\right)^2}=R\sqrt{2}\)
Mà \(Z=\frac{U}{I}=\frac{200}{2}=100\Rightarrow R=\frac{100}{\sqrt{2}}=50\sqrt{2}\)

Ta có: \(Z_C=\frac{1}{C\omega}=30\Omega\)
\(\tan\varphi=-\frac{Z_c}{R}=-\frac{1}{\sqrt{3}}\)
\(\Rightarrow\varphi=-\frac{\pi}{6}\)
\(\Rightarrow\varphi_U-\varphi_I=-\frac{\pi}{6}\Rightarrow\varphi_1=\frac{\pi}{6}rad\)
Lại có: \(I=\frac{U}{Z}=2\sqrt{2}\left(A\right)\)
\(\Rightarrow i=2\sqrt{2}\cos\left(100\pi t+\frac{\pi}{6}\right)\left(A\right)\)
Đáp án A
Vì 2 tổng đại số của hiệu điện thể 2 đoạn bằng đúng hiệu điện thế của 2 đầu mạch nên 2 hiệu điện thế này cùng pha với nhau và cùng pha với hiệu điện thế toàn mạch
Do đó ta có
\(\frac{Z_{L_1}}{L_2}=\frac{Z_{L2}}{L_2}\)
Suy ra \(Z_{L_2}=\frac{\omega L_1}{R_1}R_2=50\sqrt{3}\Omega\)
Góc nghiêng so với cường độ dòng là
\(\tan\alpha=\frac{Z_1}{R_1}=\sqrt{3}\) suy ra \(\alpha=\pi\text{/}3\)
Tổng kháng toàn mạch sẽ là
\(Z=\frac{R_1+R_2}{\cos\pi\text{/}3}=300\Omega\)
Biểu thức cường độ dòng sẽ là
\(i=0,5\sqrt{2}\cos\left(100\pi t-\pi\text{/}3\right)A\)
\(Z_L=100\sqrt 3\Omega\)
Vì \(Z_{AB}=Z_{AM}+Z_{MB}\)
Nên \(u_{AM}\) cùng pha với \(u_{MB}\)
\(\Rightarrow \tan\varphi_{AM}=\tan\varphi_{MB}\)
\(\Rightarrow \dfrac{Z_{L1}}{R_1}=\dfrac{Z_{L2}}{R_2}\)
\(\Rightarrow \dfrac{Z_{L1}}{100}=\dfrac{100\sqrt 3}{50}\)
\(\Rightarrow Z_{L1}=200\sqrt 3\Omega\)
Tổng trở \(Z=\sqrt{(100+50)^2+(200\sqrt 3+100\sqrt 3)^2}=150\sqrt{13}\Omega\)
Cường độ dòng điện \(I_0=\dfrac{150\sqrt 2}{150\sqrt {13}}=\sqrt{\dfrac{2}{13}}(A)\)
\(\tan\varphi=2\sqrt 3\)
\(\Rightarrow \varphi = 0,857\) rad
\(\Rightarrow i=\sqrt{\dfrac{2}{13}}\cos(100\pi t-0,857)(A)\)