Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
U ¯ AB ⊥ U ¯ MB ⇒ tan φ AM tan φ BM = - 1 ⇒ - Z C R Z L r = - 1 ⇒ L = CR 2 C = L R 2 cos φ 1 = cos φ 2 ⇔ ( R + r ) ( R + r ) 2 + ω 1 L - 1 ω 1 C 2 = ( R + r ) ( R + r ) 2 + ω 2 L - 1 ω 2 C 2 cos φ 1 = 1 α 1 ω 2 L = CR 2 C = L R 2 1 ω 1 C = R ω 2 ω 1 ω 1 L = R ω 1 ω 2 ⇒ LC = ( R + r ) ( R + r ) 2 + ( R ω 1 ω 2 - R ω 2 ω 1 ) 2 = 2 4 + ( ω 1 ω 2 - ω 2 ω 1 ) 2 = 0 , 96
Chọn D
tanφAB. tanφAM = -1 ⇔ Z L - Z C R . Z L R = -1
⇔ R2=ZL(ZC – ZL) = ωL( 1 ω C - ω L )
⇔ R2= L C - ω 2 L 2 ⇔ ω = L - R 2 C L 2 C
Đáp án B
+ Điều chỉnh R để công suất trên biến trở đạt cực đại 
+ Tổng trở của đoạn mạch AB là 
Để Z chia hết cho 40 thì: 
= số nguyên → r phải là bội số của 10 : r=10k
+ Hệ số công suất của đoạn mạch AB là: 
Phương pháp: Mạch điện xoay chiều có R thay đổi
Cách giải: Đáp án D
Điều chỉnh R đến giá trị 80Ω thì công suất tiêu thụ trên biến trở cực đại
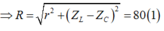
do tổng trở của đoạn mạch là số nguyên và chia hết cho 40 ⇒ Z AB = 40 n (n là số nguyên)
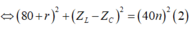
Từ (1) và (2) ta có:
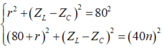
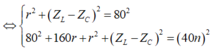
Hệ số công suất của đoạn MB là:
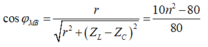
Có:
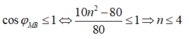
+ Với n = 4 
+ Với n = 3
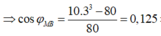
=> Chọn D
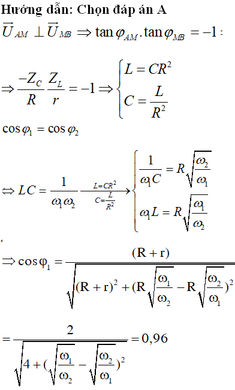
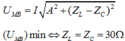
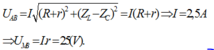
Chuẩn hóa R + r = 1.
→ Hệ số của suất của mạch
cos φ = 2 13 = 1 1 + ω 1 ω 2 − ω 2 ω 1 2 ⇒ ω 1 ω 2 = 1 4
Từ đó ta tìm được ω 1 = 40 r a d / s .
Đáp án A