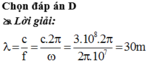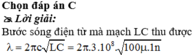Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạch LC có i vuông qua với q nên:
\((\dfrac{i}{I_0})^2+(\dfrac{q}{Q_0})^2=1\)\(\Rightarrow (\dfrac{i}{\omega Q_0})^2+(\dfrac{q}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega Q_0})^2+(\dfrac{q_1}{Q_0})^2=1\)
\((\dfrac{i_2}{\omega Q_0})^2+(\dfrac{q_2}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega })^2+(q_1)^2=(\dfrac{i_2}{\omega })^2+(q_2)^2\)
\(\Rightarrow \omega ^2=\dfrac{i_1^2-i_2^2}{q_2^2-q_1^2}\)
\(\Rightarrow T=\dfrac{2\pi}{\omega}=2\pi.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
\(\Rightarrow \lambda = c.T =2\pi c.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
Chọn B.

Tụ xoay có điện dung tỉ lệ với hàm số bậc nhất đối với góc xoay α => C = aα + b (a, b là hằng số)
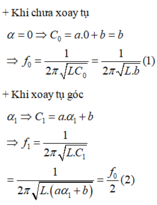
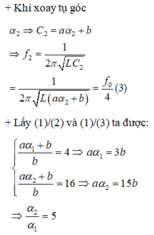
Đáp án D

Đáp án A
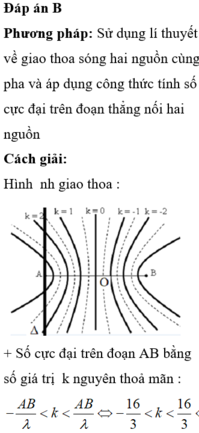
Phương pháp: Điều kiện có sóng dừng trên dây hai đầu cố định l = k λ 2 = k v 2 f (số nút = k+1)
Cách giải:
+ Trên dây có 5 nút sóng ⇒ l = 4 λ 2 = 4 v 2 . 27 = 2 v 27
+ Trên dây có 11 nút sóng ⇒ l = 10 λ 2 = 10 v 2 f = 5 v f
Từ (1) và (2) 2 v 27 = 5 v f ⇒ f = 67 , 5 H z

Bước sóng: \(\lambda=c.2\pi\sqrt{LC}\)
Để bước sóng giảm 2 lần thì điện dung giảm 4 lần, còn là 1nF, do vậy cần mắc nối tiếp C' với C.
\(\Rightarrow\frac{1}{C_b}=\frac{1}{C}+\frac{1}{C'}\Leftrightarrow\frac{1}{1}=\frac{1}{4}+\frac{1}{C'}\Rightarrow C'=\frac{4}{3}nF\)