Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tam giác ABC nội tiếp đường tròn (O) có AB là đường kính của đường tròn nên tam giác ABC là tam giác vuông(Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó.....)
b/ Vì D là giao điểm hai tiếp tuyến tại A và C của đường tròn (O) nên: DA=DC
D1=D2(t/c 2 tiếp tuyến cắt nhau)
Xét tam giác DHA=DHC(c.g.c).....nênH1=H2
Mà H1+H2=180....nên H1=H2=90...

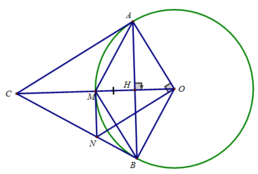
d) Ta có: CA ⊥ OA (CA là tiếp tuyến của (O)
và ON ⊥ OA (gt)
⇒ CA // ON ⇒ ∠(CON) = ∠(ACO) (sole trong)
Mà ∠(ACO) = ∠(BCO) (ΔOAC = ΔOBC)
⇒ ∠(CON) = ∠(BCO) ⇒ ΔNCO cân tại N
Xét tam giác CAO vuông tại A có ∠(AOC) = 60o( ΔAMO đều) nên:
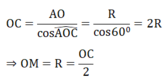
⇒ M là trung điểm của OC
ΔNCO cân tại N có NM là trung tuyến ⇒ NM cũng là đường cao
Hay NM là tiếp tuyến của (O)

a: Ta có: ΔOMN cân tại O
mà OH là đường cao
nên H là trung điểm của MN
Ta có: MN là trung trực của OA
nên H là trung điểm của OA
Xét ΔMOA có
MH vừa là đường cao, vừa là trung tuyến
nên ΔMOA cân tại M
mà OM=OA
nen ΔMOA đều
b: Xét (O) có
SM,SN là các tiếp tuyến
nên SM=SN
mà OM=ON
nên OS là trung trực của MN(1)
vì HM=HN
nên H nằm trên đừog trung trực của MN(2)
Từ (1) và (2) suy ra O,H,S thẳng hàng
mà O,H,A thẳng hàng
nên O,A,S thẳng hàng
