Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
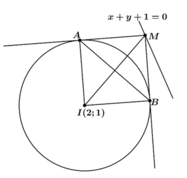
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
![]()
- Ta có :
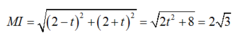
- Do đó : 2t2+ 8= 12
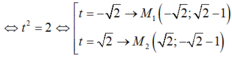

Chắc là N? Vì M mà sao đằng sau lại là \(NA^2+NB^2\)?
Do N thuộc \(\Delta\) nên tọa độ có dạng \(N\left(6t;4t+2\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AN}=\left(6t-1;4t\right)\\\overrightarrow{BN}=\left(6t+3;4t-3\right)\end{matrix}\right.\)
\(\Rightarrow NA^2+NB^2=\left(6t-1\right)^2+16t^2+\left(6t+3\right)^2+\left(4t-3\right)^2=104t^2+19\ge19\)
Dấu "=" xảy ra khi \(t=0\Rightarrow N\left(0;2\right)\)

d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)

A thuộc d và B thuộc d'?
Do \(A\in d\Rightarrow A\left(a;2a+1\right)\)
\(B\in d'\Rightarrow B\left(b;1-b\right)\)
G là trọng tâm tam giác OAB
\(\Rightarrow\left\{{}\begin{matrix}x_A+x_B+x_O=3x_G\\y_A+y_B+y_O=3y_G\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a+1+1-b=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a-b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{7}{3}\\b=\frac{11}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(\frac{7}{3};\frac{17}{3}\right)\\B\left(\frac{11}{3};-\frac{8}{3}\right)\end{matrix}\right.\)
Phương trình tham số d: \(\left\{{}\begin{matrix}x=t\\y=1-t\end{matrix}\right.\)
M thuộc d nên tọa độ có dạng \(M\left(t;1-t\right)\)
Khoảng cách từ M đến \(\Delta\): \(\dfrac{\left|4t+3\left(1-t\right)+1\right|}{\sqrt{4^2+3^2}}=2\)
\(\Leftrightarrow\left|t+4\right|=10\Rightarrow\left[{}\begin{matrix}t=6\\t=-14\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(6;-5\right)\\M\left(-14;15\right)\end{matrix}\right.\)