Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Gọi đơn chất halogen là X2
\(Cu+X_2\underrightarrow{^{to}}CuX_2\)
Ta có:
\(n_X=\frac{5,6}{22,4}=0,25\left(mol\right)=n_{CuX2}\)
\(\Rightarrow M_{CuX2}=64+2X=\frac{33,75}{0,25}=135\)
\(\Rightarrow X=35,5\left(Clo\right)\)
Halogen là Cl2 - Clo
Câu 2:
\(PTHH:Fe+2HCl\rightarrow FeCl_2+H_2\)
_______0,15__0,3___0,15___0,15__
\(n_{Fe}=\frac{8,4}{56}=0,15\left(mol\right)\)
a,\(V_{H2}=0,15.22,4=3,36\left(l\right)\)
b, \(CM_{HCl}=\frac{0,3}{0,2}=1,5M\)

Bảo toàn khối lượng ta có: $m_{R}=2,4(g)$$R+X_2\rightarrow RX_2$
Ta có: $\frac{2,4}{R}=\frac{4,26}{2X}$
Lập bảng biện luận thông qua halogen tìm được X và R lần lượt là Cl và Ca

\(m_{HX}=\dfrac{10,95.200}{100}=21,9\left(g\right)\)
\(n_{Al}=\dfrac{5,4}{27}=0,2\left(mol\right)\)
PTHH: 2Al + 6HX --> 2AlX3 + 3H2
0,2--->0,6-------------->0,3
=> \(M_{HX}=\dfrac{21,9}{0,6}=36,5\left(g/mol\right)\)
=> X là Cl
VH2 = 0,3.22,4 = 6,72(l)

1.
Gọi hóa trị của kim loại M là n, ta có:
\(2M+nCl_2\underrightarrow{^{to}}2MCl_n\)
Dựa vào pt, ta thấy:
nM=nMCln
⇔ 3,2/M=6,75/M+35,5n
⇔ M=32n
Vì M là kim loại nên hóa trị có thể là I, II và III:
- Nếu n=1 ==> M=32 (Loại)
- Nếu n=2 ==> M=64 (Chọn - Cu)
- Nếu n=3 ==> M=96 (Loại)
Vậy kim loại M là Cu.
2.
\(Cu+X_2\underrightarrow{^{to}}CuX_2\)
nX2=2,24/22,4=0,1 (mol)
nCuX2=nX2=0,1 (mol)
==> mCuX2= 0,1.(64 + 2X)=22,4
==> X= 80 (Br)
Vậy halogen X là Br.

1)
CTHH MXn
\(n_{X_2}=\dfrac{0,896}{22,4}=0,04\left(mol\right)\)
=> \(n_{MX_n}=\dfrac{0,08}{n}\left(mol\right)\)
=> \(n_{AgX}=0,08\left(mol\right)\)
=> \(M_{AgX}=\dfrac{11,48}{0,08}=143,5\left(g/mol\right)\) => MX = 35,5 (g/mol)
=> X là Cl
2)
\(n_{MCl_n}=\dfrac{0,08}{n}\left(mol\right)\)
\(n_M=\dfrac{0,96}{M_M}\left(mol\right)\)
=> \(\dfrac{0,08}{n}=\dfrac{0,96}{M_M}\)
=> MM = 12n (g/mol)
Xét n = 1 => Loại
Xét n = 2 => MM = 24 (g/mol) => M là Mg
Xét n = 3 => Loại
Vậy M là Mg
M' có hóa trị II
\(n_{O_2}=\dfrac{4,162-0,96-2,242}{32}=0,03\left(mol\right)\)
PTHH: 2Mg + O2 --to--> 2MgO
0,04-->0,02------>0,04
2M' + O2 --to--> 2M'O
0,02<-0,01------>0,02
=> MM' = \(\dfrac{2,242}{0,02}=112\left(g/mol\right)\)
a) \(\left\{{}\begin{matrix}\%n_M=\dfrac{0,04}{0,04+0,02}.100\%=66,67\%\\\%n_{M^{\cdot}}=100\%-66,67\%=33,33\%\end{matrix}\right.\)
b) \(\dfrac{M_M}{M_{M^{\cdot}}}=\dfrac{24}{112}=\dfrac{3}{14}\)
c) \(n_O=0,06\left(mol\right)\)
=> \(n_{H_2O}=0,06\left(mol\right)\)
=> \(n_{H_2SO_4}=0,06\left(mol\right)\)
=> \(C_{M\left(H_2SO_4\right)}=\dfrac{0,06}{0,5}=0,12M\)

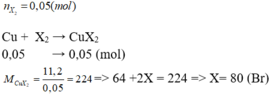
Gọi halogen đó là X , CTTQ: CuX2
\(PTHH:Cu+X_2\underrightarrow{^{to}}CuX_2\)
Áp dụng ĐLTL ta có:
\(\Leftrightarrow\frac{22,4}{5,6}=\frac{64+2X}{33,75}\)
\(\Rightarrow x=35,5\left(Clo\right)\)
Vậy halogen là Clo ( Clo )