Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) 2,5,7 chỉ có nhiêu đó thôi
b)3,11 thôi
mình chỉ chắc 70% thôi vì mình cũng là học sinh lớp 7 thầy mới chỉ
Lời giải:
$A=0,1+0,0(2453)=\frac{1}{10}+\frac{2453}{99990}=\frac{566}{4545}$ (đây đã là dạng tối giản)
Vậy số nguyên k nguyên dương nhỏ nhất để $kA$ nguyên là $4545$
![[IMG]](http://s93.photobucket.com/albums/l55/toc_xu09/tuoi%20tho/th_f-2.gif "Click this image to show the full-size version.")
gọi abc là chu kì của số thập phân vô hạn tuần hoàn đơn ( 0 < abc < 999 ) thì phân số phải tìm là : \(\frac{\overline{abc}}{999}\)
\(\frac{\overline{abc}}{999}=\frac{\overline{abc}}{3^3.37}=\frac{\overline{abc}.37^2}{3^3.37^3}=\frac{\overline{abc}}{\left(3.37\right)^3}\)
ta đặt \(\frac{\overline{abc}}{\left(3.37\right)^3}=\frac{x^3.37^3}{\left(3.37\right)^3}\)với x \(\in\)N*
\(\Rightarrow\)abc . 372 = x3 . 373
\(\Rightarrow\)abc = 37x3 < 999
\(\Rightarrow\)x3 \(\in\){ 1 ; 8 }
\(\Rightarrow\)x \(\in\){ 1 '; 2 }
\(\Rightarrow\)abc \(\in\){ 037 ; 296 }
vậy phân số cần tìm là : \(\frac{037}{999}=\frac{1}{27};\frac{296}{999}=\frac{8}{27}\)
Gọi a là chu kì.
Vì phân số mẹ bé hơn 1 nên số thập phân đó là : 0, (a)
Phân tích ra được: 0,(a) =0 + a x\(\frac{1}{999}\) =\(\frac{a}{999}\)
Ta có : \(\frac{a}{999}\)= \(\frac{a}{3^3.37}\) = \(\frac{a.37^2}{\left(3.37\right)^3}\)
Theo đề : phân số mẹ là lập phương của một số nên\(\frac{a.37^2}{\left(3.37\right)^3}\) =\(\frac{x^3.37^3}{\left(3.37\right)^3}\)
Vậy a . 372 = x3 . 373 hay a = x3 . 37 <999\(\Rightarrow\) x = 1;2
Vậy A sẽ bằng 37;296
Đáp số : 37;296
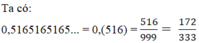
Khi đó tử số nhỏ hơn mẫu số số đơn vị là 333-172 = 161 đơn vị
Đáp án cần chọn là D
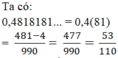
Khi đó tử số nhỏ hơn mẫu số số đơn vị là 110 -53 = 57 đơn vị
Đáp số cần chọn là D