Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
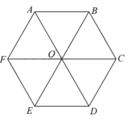
Ta có phép quay
Q O ; α A = E ⇔ O A = O E O A ; O E = α ⇒ α = A O E ^ = 120 °

Đáp án C
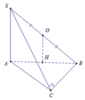
Do B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ S A C ⇒ B C ⊥ S C
Do đó O là trung điểm của SB. Do đó H là hình chiếu vuông góc của O lên m p A B C ⇒ H là trung điểm của AB

Đáp án A
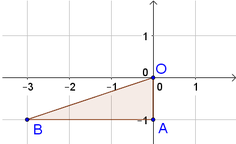
Đường thẳng cắt các trục tọa độ tại các điểm A 6 ; 0 ; B 0 ; 3
Phép quay tâm O góc 90 ∘ biến điểm A và B lần lượt thành các điểm A ' 0 ; 6 và B ' − 3 ; 0
Khi đó n A ' B ' → = 2 ; − 1 ⇒ A ' B ' : 2 x − y + 6 = 0.

Đáp án A
Vì I là tâm đối xứng của đồ thị C ⇒ I 2 ; 2
Gọi M x 0 ; 2 x 0 − 1 x 0 − 2 ∈ C ⇒ y ' x 0 = − 3 x 0 − 2 2 suy ra phương trình tiếp tuyến Δ là
y − y 0 = y ' x 0 x − x 0 ⇔ y − 2 x 0 − 1 x 0 − 2 = − 3 x 0 − 2 2 x − x 0 ⇔ y = − 3 x 0 − 2 2 + 2 x 0 2 − 2 x 0 + 2 x 0 − 2 2
Đường thẳng Δ cắt TCĐ tại A 2 ; y A → y A = 2 x 0 + 2 x 0 − 2 ⇒ A 2 ; 2 x 0 + 2 x 0 − 2
Đường thẳng Δ cắt TCN tại B x B ; 2 → x B = 2 x 0 − 2 ⇒ B 2 x 0 − 2 ; 2
Suy ra I A = 6 x 0 − 2 ; I B = 2 x 0 − 2 → I A . I B = 6 x 0 − 2 .2 x 0 − 2 = 12
Tam giác IAB vuông tại I ⇒ R Δ I A B = A B 2 = I A 2 + I B 2 2 ≥ 2 I A . I B 2 = 6
Dấu bằng xảy ra khi và chỉ khi I A = I B ⇔ 3 = x 0 − 2 2 ⇔ x 0 = 2 + 3 x 0 = 2 − 3
Suy ra phương trình đường thẳng Δ và gọi M, N lần lượt là giao điểm của Δ với Ox, Oy
Khi đó M 2 x 0 2 − 2 x 0 + 2 3 ; 0 , N 0 ; 2 x 0 2 − 2 x 0 + 2 3 ⇒ S Δ O M N = 1 2 O M . O N
Vậy S m a x = 14 + 8 3 ≈ 27 , 85 ∈ 27 ; 28 k h i x 0 = 2 + 3

Đáp án A.
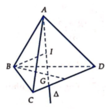
Gọi I là tâm mặt cầu ngoại tiếp ABCD ⇒ I ∈ Δ và I A = I B = R
Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất <=> IB nhỏ nhất
⇔ I B ⊥ Δ ⇔ I ≡ G ⇒ I A = I B = B G = a 3 3 = A G ⇒ V A B C D = 1 3 S B C D . A G = 1 3 . 1 2 . a . a 3 2 . a 3 3 = a 2 12

Đáp án B
y ' = 3 x 2 + 6 x ;
Phương trình tiếp tuyến của (C) tại điểm x 0 = 0 là Δ : y = − 1 .
Giao điểm của (C) và Δ là nghiệm của hệ phương trình
y = − 1 y = x 3 + 3 x 2 − 1 ⇔ x 3 + 3 x 2 − 1 = − 1 y = − 1 ⇔ x = 0 x = − 3 y = − 1
Do đó giao điểm B − 3 ; − 1 .
Tam giác OAB vuông tại A nên S O A B = 1 2 . O A . A B = 1 2 .1.3 = 3 2 .


a) Xét tam giác ACB, có CO là trung tuyến. Lại có \(CO=OA=OB=\frac{AB}{2}\), vậy nên tam giác ACB vuông lại C.
b) Xét tam giác vuông ACB, ta có:
\(\sin\widehat{CAB}=\frac{BC}{BA}=\frac{1}{2}\Rightarrow\widehat{CAB}=30^o\)
Xét tam giác vuông ACB, ta có:
\(cos\widehat{CAB}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}\Rightarrow AC=R\sqrt{3}\)
Xét tam giác vuông ABD, ta có:
\(\tan\widehat{DAB}=\frac{BD}{AB}=\frac{\sqrt{3}}{3}\Rightarrow BD=\frac{2\sqrt{3}R}{3}\)
c) Ta thấy ngay tam giác BCD vuông tại C nên tâm đường tròn ngoại tiếp tam giác BCD là trung điểm cạnh huyền.
Vậy O' là trung điểm BD.
Xét tam giác OCO' và OBO' có:
O'C = O'B (gt)
OC = OB (= R)
OO' chung
\(\Rightarrow\Delta OCO'=\Delta OBO'\left(c-c-c\right)\)
\(\Rightarrow\widehat{O'CO}=\widehat{OBO'}=90^o\)
Vậy nên O'C là tiếp tuyến của đường tròn (O).
Lại có AB vuông góc với O'B tại B nên AB là tiếp tuyến tại B của đường tròn (O').
d) Gọi H là hình chiếu của I trên OB.
\(AD=\sqrt{AB^2+BD^2}=\frac{4R\sqrt{3}}{3}\)
Ta có hai công thức tính diện tích tam giác:
Công thức Hê-rông: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) với a, b, c là độ dài các cạnh của tam giác, p là nửa chu vi
\(S=pr\) với r bán kính đường tròn nội tiếp.
Vậy nên \(r=\sqrt{\frac{\left(p-AB\right)\left(p-BD\right)\left(p-AD\right)}{p}}\)
\(p=\frac{AD+DB+BA}{2}=\left(1+\sqrt{3}\right)R\)
Vậy thì:
\(r=R\sqrt{\frac{4-2\sqrt{3}}{3}}=\frac{3-\sqrt{3}}{3}R\)
Thấy ngay IH = r.
Xét tam giác HIB có góc H vuông, \(\widehat{IBH}=45^o\) (Do BI là phân giác góc vuông)
Vậy nên \(IH=HB=\frac{3-\sqrt{3}}{3}R\)
\(\Rightarrow OH=R-HB=\frac{R\sqrt{3}}{3}\)
Xét tam giác vuông OIH, ta có:
\(OI=\sqrt{OH^2+IH^2}=R\sqrt{\frac{5-2\sqrt{3}}{3}}\)

a) Xét tam giác ACB, có CO là trung tuyến. Lại có \(CO=OA=OB=\frac{AB}{2}\), vậy nên tam giác ACB vuông lại C.
b) Xét tam giác vuông ACB, ta có:
\(\sin\widehat{CAB}=\frac{BC}{BA}=\frac{1}{2}\Rightarrow\widehat{CAB}=30^o\)
Xét tam giác vuông ACB, ta có:
\(cos\widehat{CAB}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}\Rightarrow AC=R\sqrt{3}\)
Xét tam giác vuông ABD, ta có:
\(\tan\widehat{DAB}=\frac{BD}{AB}=\frac{\sqrt{3}}{3}\Rightarrow BD=\frac{2\sqrt{3}R}{3}\)
c) Ta thấy ngay tam giác BCD vuông tại C nên tâm đường tròn ngoại tiếp tam giác BCD là trung điểm cạnh huyền.
Vậy O' là trung điểm BD.
Xét tam giác OCO' và OBO' có:
O'C = O'B (gt)
OC = OB (= R)
OO' chung
\(\Rightarrow\Delta OCO'=\Delta OBO'\left(c-c-c\right)\)
\(\Rightarrow\widehat{O'CO}=\widehat{OBO'}=90^o\)
Vậy nên O'C là tiếp tuyến của đường tròn (O).
Lại có AB vuông góc với O'B tại B nên AB là tiếp tuyến tại B của đường tròn (O').
d) Gọi H là hình chiếu của I trên OB.
\(AD=\sqrt{AB^2+BD^2}=\frac{4R\sqrt{3}}{3}\)
Ta có hai công thức tính diện tích tam giác:
Công thức Hê-rông: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) với a, b, c là độ dài các cạnh của tam giác, p là nửa chu vi
\(S=pr\) với r bán kính đường tròn nội tiếp.
Vậy nên \(r=\sqrt{\frac{\left(p-AB\right)\left(p-BD\right)\left(p-AD\right)}{p}}\)
\(p=\frac{AD+DB+BA}{2}=\left(1+\sqrt{3}\right)R\)
Vậy thì:
\(r=R\sqrt{\frac{4-2\sqrt{3}}{3}}=\frac{3-\sqrt{3}}{3}R\)
Thấy ngay IH = r.
Xét tam giác HIB có góc H vuông, \(\widehat{IBH}=45^o\) (Do BI là phân giác góc vuông)
Vậy nên \(IH=HB=\frac{3-\sqrt{3}}{3}R\)
\(\Rightarrow OH=R-HB=\frac{R\sqrt{3}}{3}\)
Xét tam giác vuông OIH, ta có:
\(OI=\sqrt{OH^2+IH^2}=R\sqrt{\frac{5-2\sqrt{3}}{3}}\)

Đáp án C