Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
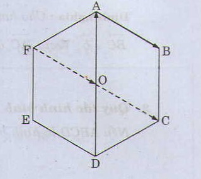
Số các véc tơ khác \(\overrightarrow{0}\) bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FO};\overrightarrow{OF};\overrightarrow{ED};\overrightarrow{DE};\overrightarrow{FC};\overrightarrow{CF}\).
Có 8 véc tơ.

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
Các véc tơ bằng véc tơ \(\overrightarrow{AB}\) là:
\(\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\).

TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
Do các tam giác OAB, OCD, OED, OEF, OFA , OBC cùng là tam giác đều nên OA = OB = OC = OD = OE = OF = 6cm.
Do \(\overrightarrow{i}\) và \(\overrightarrow{OD}\) cùng hướng nên D(6;0), A (0;-6).
Áp dụng hệ thức lượng trong tam giác vuông ta được:\(EC=2.DC.sin60^o=2.6.\dfrac{\sqrt{3}}{2}=6\sqrt{3}\).
\(\overrightarrow{EC}\) cùng hướng với \(\overrightarrow{j}\) nên:
Suy ra \(y_B=y_C=3\sqrt{3}\); \(y_E=y_F=-3\sqrt{3}\).
Do BC = 6cm và BC // OD nên \(x_E=x_C=3;x_F=x_B=-3\).
Vậy \(A\left(-6;0\right);D\left(6;0\right);B\left(-3;3\sqrt{3}\right),C\left(3;3\sqrt{3}\right)\);\(E\left(3;-3\sqrt{3}\right)\)\(F\left(-3;-3\sqrt{3}\right)\) .

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
Các véc tơ bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là: \(\overrightarrow{FO};\overrightarrow{AB};\overrightarrow{ED}\).
Vậy có 3 véc tơ.

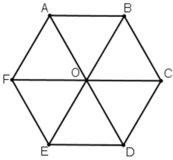
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
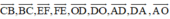
b) Các vectơ bằng vectơ AB→ là:
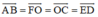

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
a)
\(\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}=\overrightarrow{AB}+\overrightarrow{AF}\).
Vậy \(\overrightarrow{AD}=2\overrightarrow{AO}=2\left(\overrightarrow{AB}+\overrightarrow{AF}\right)\).
b)
\(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{1}{2}\overrightarrow{AC}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\).
A B C a H
Do tam giác ABC cân tại B nên BH là đường cao, đường trung tuyến, đường phân giác ứng với đỉnh B của tam giác ABC.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AH=AB.sin60^o=\dfrac{a\sqrt{3}}{2}\).
\(AC=2BH=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\)\(=a\sqrt{3}\).

TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
D = (10.28, -5.54)
D = (10.28, -5.54)
D = (10.28, -5.54)
F = (9.98, -5.84)
F = (9.98, -5.84)
F = (9.98, -5.84)
H = (10.64, -5.76)
H = (10.64, -5.76)
H = (10.64, -5.76)
I = (-4.38, -5.94)
I = (-4.38, -5.94)
I = (-4.38, -5.94)
J = (10.98, -5.94)
J = (10.98, -5.94)
J = (10.98, -5.94)
L = (10.42, -6.1)
L = (10.42, -6.1)
L = (10.42, -6.1)
N = (10.76, -6)
N = (10.76, -6)
N = (10.76, -6)
O = (-4.3, -5.82)
O = (-4.3, -5.82)
O = (-4.3, -5.82)
P = (11.06, -5.82)
P = (11.06, -5.82)
P = (11.06, -5.82)
R = (10.96, -5.94)
R = (10.96, -5.94)
R = (10.96, -5.94)
Dễ thấy

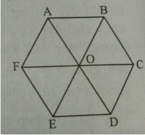
Do ABCDEF là lục giác đều tâm O nên AB = BC = CD= DE = EF = FA = OC.
Trên hình có tất cả 12 đoạn thẳng bằng nhau và bằng OC, tạo thành 24 vectơ có độ dài bằng OC. Trừ ra vectơ O C → còn lại 23 vectơ.
Chọn D.

Chọn C.
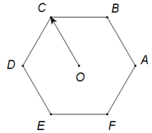
Các vecto cùng phương với ![]() có điểm đầu và điểm cuối là các đỉnh của lục giác :
có điểm đầu và điểm cuối là các đỉnh của lục giác : ![]()
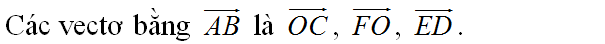
a) Các vec tơ cùng phương với vec tơ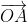 :
:
b) Các véc tơ bằng véc tơ :
: 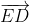 ;
; 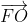 ;
; 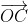 .
.