

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




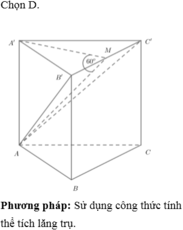
Gọi H chân đường kẻ từ A của lăng trụ
Khi đó A'H là là hình chiếu của AA' trên mp
Xét tam giác AA'H vuông tại H có : \(SinA'=\frac{AH}{AA'}\)
\(AH=AA'.SinA'=AA'.Sin60^o=\frac{b\sqrt{3}}{2}\)
Do tam giác A'B'C' là tam giác đều nên chiều cao của tam giác : \(\frac{a\sqrt{3}}{2}\)
Thể tích ABC.A'B'C' : V = \(\frac{1}{3}\). AH . \(S_{A'B'C'}=\frac{3}{8}\)\(a^2b\)
Đáp án đó

Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít