Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
Gọi là trung M điểm của BC
Chứng minh được BC ⊥ (AA'M) . Do đó góc giữa hai mặt phẳng (A'BC) và mặt phẳng (ABC) là góc A ' M A ^ = 30 o
Đặt AB = x
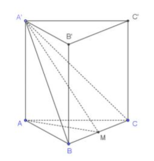
Tam giác là hình ABC chiếu của tam giác A'BC lên mặt phẳng (ABC)
![]()
![]()
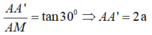
![]()

Chọn C
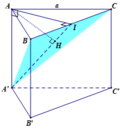
Gọi I là trung điểm của BC và H là hình chiếu vuông góc của A trên A'I. Khi đó ta có:
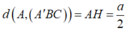
Trong tam giác vuông AA'I ta có:
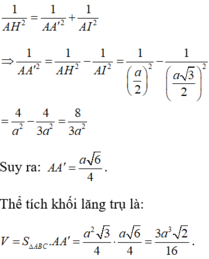

Đáp án A.
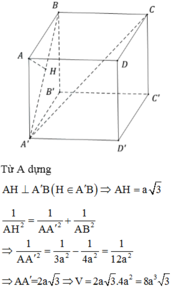
Từ A dựng A H ⊥ A ' B ( H ∈ A ' B )
⇒ A H = a 3
1 A H 2 = 1 A A ' 2 + 1 A B 2
⇒ 1 A A ' 2 = 1 3 a 2 - 1 4 a 2 = 1 12 a 2
⇒ A A ' = 2 a 3 ⇒ V = 8 a 3 3

Chọn D.
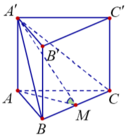
Gọi độ dài cạnh AA' = x (x > 0)
Xét ∆ A'AM vuông tại ta có:

Xét
∆
ABC đều có đường cao ![]()
Ta có: ![]()
![]()
![]()
Vậy AA' = 1, AB = 2. Do đó 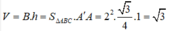



Hình bạn tự vẽ nhé
gọi M là trung điểm cạnh BC
vì là lăng trụ tam giác đều nên tam giác A'BC cân tại A' \(\Rightarrow\) A'M vuông góc với BC và AM vuông góc với BC
=> (AA'M) vuông góc ( A'BC) => góc giữa AA' và (A'BC) = góc giữa AA' và A'M = 300
xét tam giác AA'M vuông tại A có: tan30 = \(\frac{AM}{AA'}\) => AM = \(\frac{\sqrt{3}a}{3}\)
=> cạnh tam giác = \(\frac{2a}{3}\) => SABC= \(\frac{\sqrt{3}a^2}{18}\) => VABC.A'B'C'=\(AA'\times S_{ABC}\) = \(\frac{\sqrt{3}a^3}{18}\)
mình làm vậy, không biết đúng không nữa :))