Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

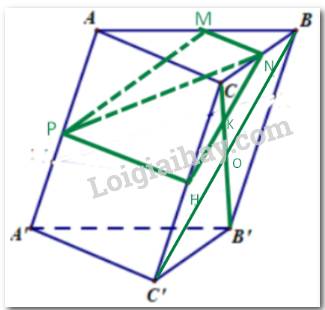
a) Ta có \(\left( {MNP} \right) \cap \left( {ABC} \right) = MN,\left( {ABC} \right) \cap \left( {ACC'A'} \right) = AC,AC//MN\) (do MN là đường trung bình của tam giác ABC) suy ra giao tuyến của (MNP) và (ACC'A') song song với MN và AC.
Qua P kẻ đường thẳng song song với AC cắt CC' tại H.
PH là giao tuyến của (MNP) và (ACC'A').
Nối H với N cắt B'C tại K.
Vậy K là giao điểm của (MNP) và B'C.
b) Gọi giao điểm BC' và B'C là O.
Ta có ACC'A' là hình bình hành P là trung điểm AA', PH //AC suy ra H là trung điểm CC'.
Xét tam giác CC'B ta có: HN là đường trung bình suy ra CK = OK.
Mà OC = OB' suy ra \(\frac{{KB'}}{{KC}} = 3\).

Ta có \(\frac{MA}{MB}=k\Leftrightarrow MA^2=k^2MB^2\Leftrightarrow\overrightarrow{MA^2}=k^2\overrightarrow{MB^2}\)
\(\Leftrightarrow\left(\overrightarrow{MA}-k\overrightarrow{MB}\right)\left(\overrightarrow{MA}+k\overrightarrow{MB}\right)=0\)
Gọi P, Q là các điểm thỏa mãn \(\overrightarrow{PA}.\overrightarrow{MQ}=0\Leftrightarrow MP\perp MQ\)
Từ đó suy ra tập hợp tất cả các điểm M cần tìm là đường tròn đường kính PQ
* Với k=1,quỹ tích cần tìm là đường trung trực (tương ứng mặt phẳng trung trực, với bài toàn trong không gian) của đoạn thẳng AB
* Đường tròn tìm được trong bài trên được gọi là đường tròn Apolonius
* Với bài toàn ở trong không gian, tương tự như vậy, ta cũng thu được quỹ tích là mặt cầu đường kính PQ, và mặt cầu đó cũng được gọi là mặt cầu Apolpnius


