Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

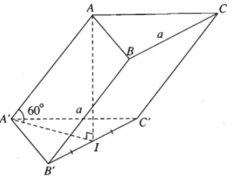
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
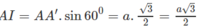
b) 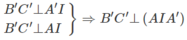
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

Chọn D

Gọi N, K là trung điểm của BB', A'B'
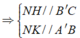
![]()
Ta tính được
![]()
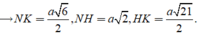
Áp dụng định lí hàm cosin ta suy ra

Cách 2. Chọn hệ trục tọa độ Oxyz với
![]()
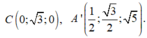
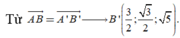

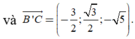
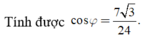

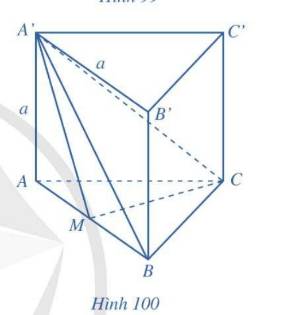
a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)

Đáp án A.
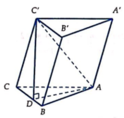
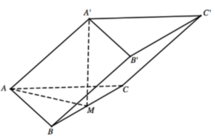
Theo giả thiết ta có CD' ⊥ (ABC). Áp dụng định lý Cô-sin cho ∆ ABD ta được:
AD = ![]()
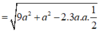
![]()
Hình chiếu vuông góc của AC’ trên mặt phẳng (ABC) là AD, vì vậy ta có góc giữa AC' và mặt phẳng (ABC) là góc C ' A D ^ = 45 0 => ∆ C'AD vuông cân tại D
![]()
Diện tích
∆
ABC là 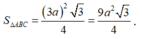
Do đó 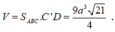

Gọi D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AD\perp BC\\AD=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
Gọi E là trung điểm BD \(\Rightarrow\) HE là đường trung bình tam giác ABD
\(\Rightarrow\left\{{}\begin{matrix}HE||AD\Rightarrow HE\perp BC\\HE=\dfrac{1}{2}AD=\dfrac{a\sqrt{3}}{4}\end{matrix}\right.\)
Mà \(B'H\perp\left(ABC\right)\Rightarrow B'H\perp BC\Rightarrow BC\perp\left(B'HE\right)\)
\(\Rightarrow\widehat{B'EH}\) là góc giữa (BCC'B') và đáy
\(\Rightarrow\widehat{B'HE}=60^0\)
\(\Rightarrow B'H=HE.tan60^0=\dfrac{3a}{4}\)
\(AA'||BB'\Rightarrow AA'||\left(BCC'B'\right)\Rightarrow d\left(AA';BC\right)=d\left(AA';\left(BCC'B'\right)\right)=d\left(A;\left(BCC'B'\right)\right)\)
Mà H là trung điểm AB \(\Rightarrow AB=2HB\Rightarrow d\left(A;\left(BCC'B'\right)\right)=2d\left(H;\left(BCC'B'\right)\right)\)
Từ H kẻ \(HK\perp B'E\)
Do \(BC\perp\left(B'HE\right)\Rightarrow\left(BCC'B'\right)\perp\left(B'HE\right)\)
Mà B'E là giao tuyến (B'HE) và (BCC'B')
\(\Rightarrow HK\perp\left(BCC'B'\right)\Rightarrow HK=d\left(H;\left(BCC'B'\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{B'H^2}+\dfrac{1}{HE^2}\Rightarrow HK=\dfrac{B'H.HE}{\sqrt{B'H^2+HE^2}}=\dfrac{3a}{8}\)
\(\Rightarrow d\left(AA';BC\right)=2HK=\dfrac{3a}{4}\)

a.
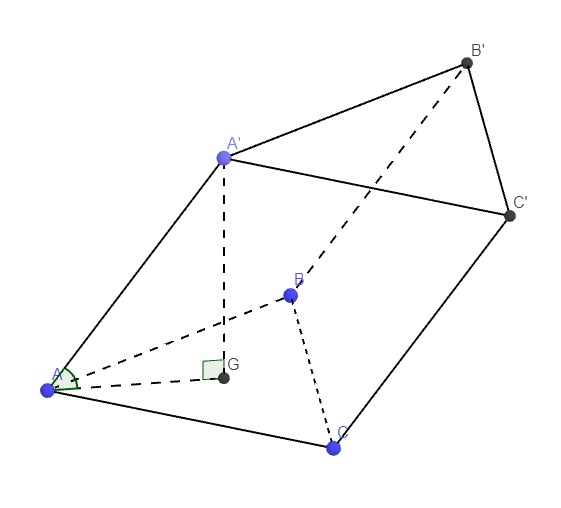
Do A' cách đều A,B,C \(\Rightarrow A'A=A'B=A'C\) hay \(A'ABC\) là chóp tam giác đều
\(\Rightarrow\) Hình chiếu vuông góc của A' lên (ABC) trùng trọng tâm ABC
Gọi G là trọng tâm ABC \(\Rightarrow A'G\perp\left(ABC\right)\)
\(\Rightarrow A'G\) là đường cao lăng trụ
Lại có \(A'G\perp\left(ABC\right)\Rightarrow AG\) là hình chiếu vuông góc của A'A lên (ABC)
\(\Rightarrow\widehat{A'AG}\) là góc giữa A'A và (ABC) \(\Rightarrow\widehat{A'AG}=60^0\)
\(AG=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'G=AG.tan60^0=a\)
b.
Đề bài thật kì quặc, ở giả thiết đã cho sẵn góc giữa A'A và (ABC) là 60 độ sao còn bắt tính?
Còn góc đó chúng ta đã xác định ở câu a là \(\widehat{A'AG}\)


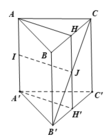
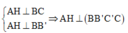
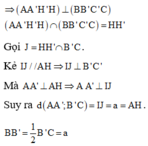

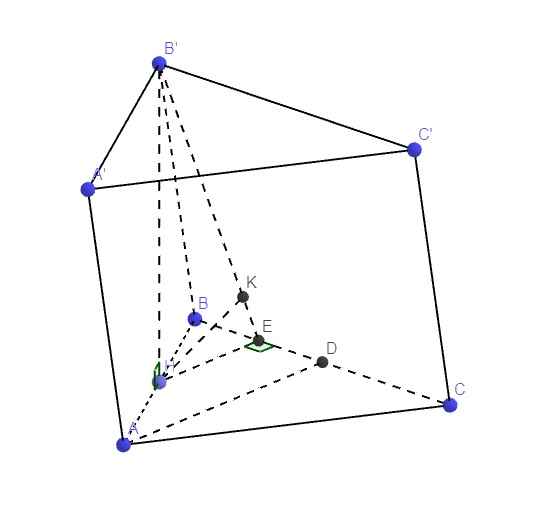
a) Có \(A'H=\dfrac{a\sqrt{3}}{2}\). Lại có \(AH\perp\left(A'B'C'\right)\) tại H nên \(\widehat{AA',\left(A'B'C'\right)}=\widehat{AA'H}=60^o\)
\(\Rightarrow AH=A'H.\tan60^o\) \(=\dfrac{a\sqrt{3}}{2}.\sqrt{3}=\dfrac{3a}{2}\)
b) Kẻ \(HK\perp A'B'\) tại K, \(HL\perp AK\) tại L.
Ta thấy \(A'B'\perp KH\) và \(A'B'\perp AH\) nên \(A'B'\perp\left(AHK\right)\)
\(\Rightarrow A'B'\perp HL\)
Mà \(HL\perp AK\) nên \(HL\perp\left(AA'B\right)\) \(\Rightarrow\left(AHK\right)\perp\left(AA'B\right)\)
Hơn nữa có \(AH\perp\left(A'B'C'\right)\) nên \(\left(AHK\right)\perp\left(A'B'C'\right)\)
Do đó góc nhị diện \(\left[A,A'B',C'\right]\) chính là \(\widehat{AKH}\)
Ta có \(\dfrac{1}{HK^2}=\dfrac{1}{HA'^2}+\dfrac{1}{HB'^2}\) \(=\dfrac{1}{\left(\dfrac{a\sqrt{3}}{2}\right)^2}+\dfrac{1}{\left(\dfrac{a}{2}\right)^2}\) \(=\dfrac{16}{3a^2}\)
\(\Rightarrow HK=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow\widehat{AKH}=\tan^{-1}\left(\dfrac{AH}{KH}\right)\) \(=\tan^{-1}\left(\dfrac{\dfrac{3a}{2}}{\dfrac{a\sqrt{3}}{4}}\right)\) \(=\tan^{-1}\left(2\sqrt{3}\right)\) \(\approx73,9^o\)
Vậy ...
c) Gọi M là trung điểm BC. Khi đó dễ thấy tứ giác AMHA' là hình bình hành. Kẻ \(AX\perp HM\) tại X.
Ta có \(BC\perp AM\) và \(BC\perp AH\) nên \(BC\perp\left(AMH\right)\)
\(\Rightarrow BC\perp AX\). Lại có \(AX\perp HM\) nên \(AX\perp\left(BB'C'\right)\)
\(\Rightarrow\left(AA'HM\right)\perp\left(BB'C'\right)\)
Hơn nữa vì \(AH\perp\left(A'B'C'\right)\) nên \(\left(AA'HM\right)\perp\left(A'B'C'\right)\)
Do đó góc nhị diện \(\left[B,B'C',A'\right]\) chính là \(\widehat{A'HM}=90^o+\widehat{AHM}=90^o+\widehat{A'AH}=90^o+30^o=120^o\)
d) \(S_đ=\dfrac{a^2\sqrt{3}}{4}\)
\(\Rightarrow V_{lt}=S_đ.h\) \(=\dfrac{a^2\sqrt{3}}{4}.\dfrac{3a}{2}\) \(=\dfrac{3a^2\sqrt{3}}{8}\) (đvtt)