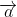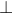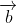Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết suy ra AB=5 và A, B trở về cùng 1 phía của đường thẳng \(\Delta\)
a) Nếu tam giác ABC cân tại C thì CA=CB và từ đó, tìm được \(C\left(-\frac{47}{4};\frac{47}{2}\right)\)
Nếu tam giác ABC cân tại C thì AC=AB=5, từ đó tìm được C(2;-4) và C(-2;4) thỏa mãn. Nếu tam giác ABC cân tại B thì BC=BA=5 nhưng \(d\left(B;\Delta\right)=\frac{16}{\sqrt{5}}>5\) nên trong trường hợp này không có điểm C thỏa mãn
b) Với I là trung điểm AB thì \(\overrightarrow{AD}+\overrightarrow{BD}=\overrightarrow{2ID}\)
Do đó \(D\in\Delta:\left|\overrightarrow{AD}+\overrightarrow{BD}\right|\) nhỏ nhất khi và chỉ khi D là hình chiếu của I trên \(\Delta\).
Vậy đáp số : \(D\left(-\frac{1}{5};\frac{2}{5}\right)\)
c) \(E\left(\frac{2}{11};-\frac{4}{11}\right)\)
d) \(\left|FA-FB\right|\ge0\),\("="\)\(\Leftrightarrow FA=FB\Leftrightarrow F\left(-\frac{47}{4};\frac{47}{2}\right)\)

a)Xét tam giác ABM và tam giác ECM![]()
MA=ME(gt)
góc AMB=góc EMC(đđ)
MB=MC(do AM là đường trung tuyến)
\(\Rightarrow\)tam giác ABM= tam giác ECM(c.g.c)
b)Vì tam giác ABM= tam giác ECM(c.g.c)
\(\Rightarrow\)CE=AB(cặp cạnh tương ứng)
Vì AB<AC(cạnh góc vuông nhỏ hơn cạnh huyền)
Mà AB=CE
\(\Rightarrow\)CE<AC
c)Vì tam giác ABM= tam giác ECM(c.g.c)
\(\Rightarrow\)BAM=MEC(cặp góc tương ứng)
Vì CE<AC\(\Rightarrow\)MEC<MAC
Mà MEC=BAM
\(\Rightarrow\)BAM<MAC(vô lí)
d)Xét tam giác AMC và tam giác EMB
MA=ME(gt)
góc AMB=góc EMC(đđ)
MB=MC(do AM là đường trung tuyến)
\(\Rightarrow\)tam giác AMC= tam giác EMB(c.g.c)
\(\Rightarrow\)ACB=EBM(cặp góc tương ứng)
\(\Rightarrow\)BE//AC vì ACB=EBM(so le trong)
e)Minh ko hiểu bạn ghi gì cả
Bạn xem lại câu c nha
Làm mất nhiều thời gian quá!

A B C K H I
a)Vì tam giác ABC vuông tại A nên AB vuông góc với AC mà HK vuông góc với AC nên AB//HK
b)Ta có: ^AHK=^AHI=900 mà HI=HK nên AH là đường trung trực của KI
=>AK=AI(tính chất đường trung trực của đoạn thẳng)
nên tam giác AKI cân tại A
c)Vì tam giác AKI cân tại A nên ^AKI=^AIK(1)
Vì AB//HK nên ^BAK=^AKI( 2 góc sole trong)(2)
Từ (1);(2) => ^BAK=^AIK
d)Vì tam giác AIK có ^AHK=^AHI=900 nên AH là đường cao của tam giác AKI mà tam giác AKI cân tại A nên AH cũng là đường phân giác của tam giác AKI(tính chất đường cao, tia phân giác, đường trung trực, đường trung tuyến của một tam giác cân từ đỉnh đến cạnh đáy đối diện) hay ^KAH=^IAH
Xét tam giác AKC và tam giác AIC có:
AC là cạnh chung
^KAH=^IAH(CMT)
AK=AI(CMT)
Do đó, tam giác AKC=tam giác AIC(c.g.c)
=>^AKC=^AIC(2 góc tương ứng)

Bài 2:
|x-m|<=1
=>-1<=x-m<=1
=>m-1<=x<=m+1
Để X là tập con của (-5;1] thì m-1>-5 và m+1<=1
=>-4<m<=0

a) A ⊂ C Ta có x chia hết cho 12 => x chia hết cho 3 và 4 => đpcm
B ⊂ C Ta có x chia hết cho 12 mà 12 chia hết cho 6 => đpcm
b) A ∪ B = { x ∈ N | x chia hết cho 4 và x chia hết cho 6 }
Vì x chia hết cho 6 và 4 => x chia hết 12 => đpcm
c ) Với x=4 thì x chia hết cho 4 thỏa mãn A
x không chia hết cho 6 không thỏa mãn B
=>A không phải là con của B.

\(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2m-3>m+1\\m+1\ge-1\\2m-3\le3\end{matrix}\right.\\\left\{{}\begin{matrix}2m-3>m+1\\m+1\ge5\\\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m>4\\m\ge-2\\m\le3\end{matrix}\right.\\\left\{{}\begin{matrix}m>4\\m\ge4\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m>4\)

a: Xét ΔDBH vuông tại H và ΔECK vuông tại K có
DB=EC
\(\widehat{DBH}=\widehat{ECK}\)
Do đó: ΔDBH=ΔECK
Suy ra: HB=CK
b: Xét ΔAHB và ΔAKC có
AB=AC
\(\widehat{ABH}=\widehat{ACK}\)
BH=CK
Do đó: ΔAHB=ΔAKC
c: Xét tứ giác HKED có
HD//KE
HD=KE
Do đó: HKED là hình bình hành
Suy ra: HK//DE
d: Xét hình bình hành HKED có \(\widehat{KHD}=90^0\)
nên HKED là hình chữ nhật
Suy ra: HE=KD
Xét ΔAHE và ΔAKD có
AH=AK
HE=KD
AE=AD
Do đó: ΔAHE=ΔAKD

a) A= { 0, 3, 6, 9, 12, 15, 18 }
b) Các phân tử của tập hợp B đều là số chẵn => B là số chẵn
a) A = {0, 3, 6, 9, 12, 15, 18}.
b) B = {x ∈ N / x = n(n+1), n ∈ N, 1 ≤ n ≤ 5}
) Ta có =
= 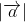 +
+ 
Nếu coi hình bình hành ABCd có =
= 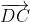 =
= 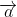 và
và 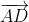 =
= 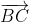 =
= 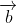 thì
thì  là độ dài đường chéo AC và
là độ dài đường chéo AC và 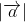 = AB;
= AB;  = BC.
= BC.
Ta lại có: AC = AB + BC
Đẳng thức xảy ra khi điểm B nằm giữa hai điểm A, C.
Vậy =
= 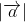 +
+  khi hai vectơ
khi hai vectơ 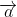 ,
, 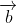 cùng hướng.
cùng hướng.
b) Tương tự, là độ dài đường chéo AC
là độ dài đường chéo AC
Hình bình hành ABCD có hai đường chéo bằng nhau nên nó là hình chữ nhật, ta có AD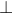 AB hay
AB hay