Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

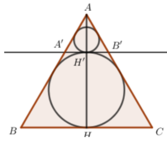
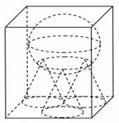
Thiết diện qua trục hình nón là 1 tam giác đều cạnh x. Do đó bán kính đường tròn nội tiếp tam giác cũng chính là bán kính mặt cầu nội tiếp chóp là



Chọn đáp án B
Thiết diện qua trục của hình nón là một tam giác đều cạnh l.
Do đó bán kính đường tròn nội tiếp tam giác cũng chính là bán kính mặt cầu nội tiếp chóp là
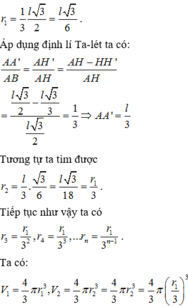


Chọn đáp án B
Phương pháp
Công thức tính thể tích của khối cầu có bán kính r: V = 4 3 πr 3 .
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 πR 2 h
Cách giải
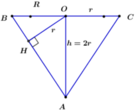
Gọi r là bán kính của khối cầu, R là bán kính của khối nón và h là chiều cao của khối nón.
Khi đó ta có: h=2r.
Theo đề bài ta có: thể tích của nửa khối cầu là:
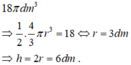
Áp dụng hệ thức lượng cho tam giác OAB vuông tại O, có đường cao OH
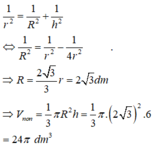

Đáp án C
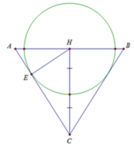
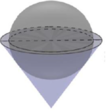
Minh họa bằng hình vẽ bên. Đặt H E = R ⇒ h = 2 R = H C
Thể tích khối cầu V 1 = 4 π R 3 3 ⇒ thể tích nước tràn ra là V = 2 π R 3 3
Lại có 1 H A 2 + 1 H C 2 = 1 H E 2 ⇒ H A = r N = 2 R 3
⇒ V N = 1 3 π r 2 h = 8 π R 3 9 = 4 V 3
Thể tích nước còn lại trong bình là 4 V 3 − V = V 3 = 6 π

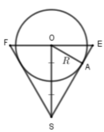
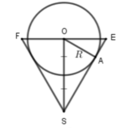
Gọi bán kính khối cầu là R ta có:
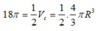
Khi đó chiều cao hình nón
h = O S = 2 R = 6 d m
Xét tam giác OES vuông tại O, đường cao OA nên
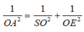
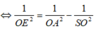
![]()
![]()
Thể tích khối nón:
![]()
Thể tích nước còn lại là:
![]()
Chọn đáp án B.
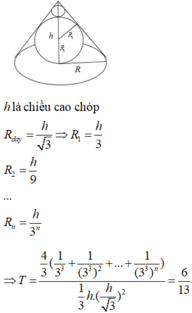


Đáp án C
Ta dễ dàng nhìn thấy quy luật của thể tích các khối cầu