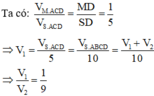
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Phương pháp:
Chia khối lập phương, nhận xét các khối tạo thành và tính thể tích của chúng
Cách giải:
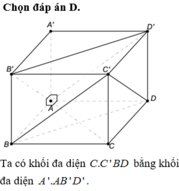
Chia khối lập phương ABC.A’B’C’ bởi mặt phẳng (AB’D’) và (C’BD) ta được:
+) Chóp A.A’B’D’
+) Chóp C’.BCD
+) Khối bát diện ABD.B’C’D’
Ta có
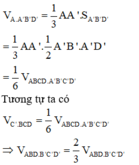
Các khối A.A’B’D’ và C’.BCD không phải là chóp tam giác đều và khối bắt diện ABD.B’C’D’ không phải là khói bát diện đều
Do đó chỉ có mệnh đề III đúng

Đáp án A
Nếu số mặt là 6 dễ thấy số cạnh là 9, nếu số mặt là 4 thì số cạnh là 6 do đó (2) sai.

Đáp án C
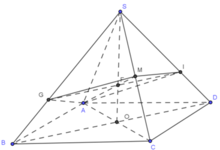
Nhìn hình vẽ ta thấy V 1 = V S . M I A G .
Gọi V S . A B C D = V
⇒ V S . A B C = V S . A D C = V 2
Có V S . A G M V S . A B C = S G S B . S M S C = 2 3 . 1 2 = 1 3
⇒ V S . A G M = V 6
Có V S . A M I V S . A D C = S M S C . S I S D = 1 2 . 2 3 = 1 3
⇒ V S . A M I = V 6
⇒ V S . M I A G = V 3 ⇒ V 2 = V − V 3 = 2 3 V ⇒ V 2 V 1 = 2

Đáp án D.
Phương pháp : Dựng thiết diện, xác định hai phần cần tính thể tích.
Sử dụng phân chia và lắp ghép các khối đa diện.
Cách giải : Gọi E = MN ∩ B'C'
Kéo dài MP cắt AB tại D, cắt AA ‘ tại F.
Nối NF, cắt AC tại G.
Do đó thiết diện của lăng trụ khi cắt bởi mặt phẳng (MNP) là NEPDG.
Gọi V1 là thể tích khối đa diện chứa đỉnh A’ ta có :
![]()
Ta có: ![]()
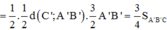
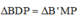
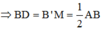
=> D là trung điểm của AB
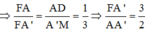
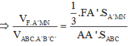
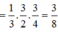
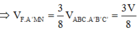
Dễ dàng chứng minh được ∆ADG đồng dạng ∆A’MN theo tỉ số 1 3
![]()
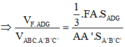
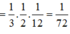
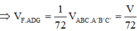
Áp dụng định lí Menelaus trong tam giác A’B’C’ ta có:
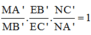
![]()
Áp dụng định lí Menelaus trong tam giác A’MN ta có:
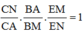
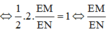
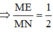
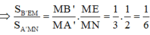
![]()
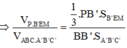
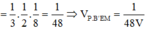
Vậy 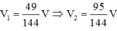
=> V 1 V 2 = 49 95

Chọn đáp án A
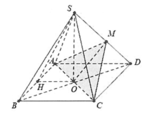
Gọi O là tâm hình vuông ABCD, H là trung điểm của AB
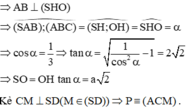
Mặt phẳng (ACM) chia khối chóp S.ABCD thành hai khối đa diện M.ACD có thể tích V1 và khối đa diện còn lại có thể tích V2