Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
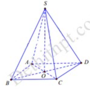
Kí hiệu như hình vẽ với S O ⊥ A B C D và tứ giác ABCD là hình vuông.
Ta có V = 1 3 S O . S A B C D = 1 3 S O . A B 2
Thể tích mới V ' = 1 3 . 1 2 S O . 3 A B 2 = 9 2 V

Đáp án A
Diện tích đáy tăng lên 9 lần và độ dài đường cao xuống hai lần. Khi đó thể tích khối chóp mới là 9 2 V

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)

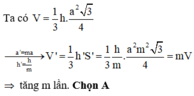



Đáp án A
Nếu tăng cạnh đáy lên 2 lần thì diện tích đáy sẽ tăng lên 4 lần. Gọi diện tích đáy lúc đầu là S ⇒ diện tích đáy sau khi tăng là 4S.
Gọi chiều cao lúc đầu là h ⇒ chiều cao sau khi giảm là h 4 ⇒ Thể tích lúc đầu bằng thể tích lúc sau = S h 3 ⇒ thể tích không thay đổi.