Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cau 12:
gọi E là trung điểm AB \(\Rightarrow\)MẸ//BC ; và EN// AC do do ME=BD/2 ;NE= AC/2
\(\Rightarrow\left[\widehat{BD;AC}\right]=\left[\widehat{ME;EN}\right]=90^0\)
\(\Delta MEN\)vuông tại E\(\Rightarrow MN^2=ME^2+NE^2=\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2=\left(\dfrac{10a^2}{4}\right)\Rightarrow MN=\dfrac{a\sqrt{10}}{2}\)
chọn đáp án A
vẽ hình ở ngoài rồi dán vào ko biết tại sao nó lại thụt xuống dưới![]()

Hướng dẫn: D
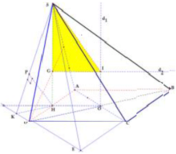
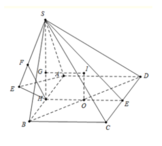
+ Gọi x > 0 là cạnh của hình vuông ABCD và H là trung điểm cạnh AD
+ Dễ dàng chứng minh
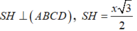
+ Gọi O = AC ∩ BD và G là trọng tâm ∆ A S D , đồng thời d 1 , d 2 lần lượt là 2 trục đường tròn ngoại tiếp ABCD, ∆ S A D ( d 1 qua O và // SH, d 2 qua G và //AB)
⇒ I = d 1 ∩ d 2 là tâm mặt cầu ngoại tiếp khối chóp S. ABCD ⇒ R = SI
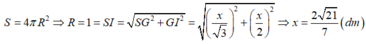
(trong video bài giảng chữa đề, phần này Thầy dùng công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp trong trường hợp chóp có mặt bên vuông góc với mặt đáy).
+ Gọi E là điểm thỏa ADEC là hình bình thành
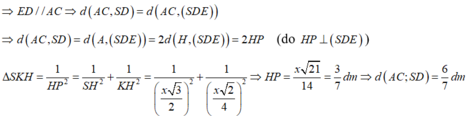

Câu 1: \(\frac{\pi}{2}<\alpha,\beta<\pi\)
=>\(\sin\alpha>0;\sin\beta>0;cos\alpha<0;cos\beta<0\)
\(\sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\sin^2\alpha=1-\left(\frac13\right)^2=\frac89\)
mà \(cos\alpha<0\)
nên \(cos\alpha=-\frac{2\sqrt2}{3}\)
Ta có: \(\sin^2\beta+cos^2\beta=1\)
=>\(\sin^2\beta=1-\left(-\frac23\right)^2=1-\frac49=\frac59\)
mà \(\sin\beta>0\)
nên \(\sin\beta=\frac{\sqrt5}{3}\)
\(\sin\left(\alpha+\beta\right)=\sin\alpha\cdot cos\beta+cos\alpha\cdot\sin\beta\)
\(=\frac13\cdot\frac{-2}{3}+\frac{-2\sqrt2}{3}\cdot\frac{\sqrt5}{3}=\frac{-\sqrt2-2\sqrt{10}}{9}\)
Câu 2:
\(P=cos\left(a+b\right)\cdot cos\left(a-b\right)\)
\(=\frac12\cdot\left\lbrack cos\left(a+b+a-b\right)+cos\left(a+b-a+b\right)\right\rbrack=\frac12\cdot\left\lbrack cos2a+cos2b\right\rbrack\)
\(=\frac12\cdot\left\lbrack2\cdot cos^2a-1+2\cdot cos^2b-1\right\rbrack=cos^2a+cos^2b-1\)
\(=\left(\frac13\right)^2+\left(\frac14\right)^2-1=\frac19+\frac{1}{16}-1=\frac{25}{144}-1=-\frac{119}{144}\)

e hk tham gia
tui đây nè-_-
tui dag nhắn mà ông bơ tui luôn
chán thấy mẹ
ông bỏ rơi tui mà còn kiu nữa
mấy nay buồn thấy mẹ

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42

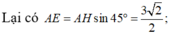
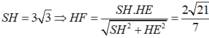
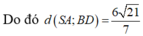






 . Tính
. Tính 

 .
. . Tính
. Tính  bằng:
bằng:
 bằng:
bằng:

 .
.
