Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3
Đáp án B
Diện tích đáy ABCD là SABCD = AB. BC = a.2a = 2a2.
Thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . 2 a . 2 a 2 = 4 a 3 3
Chọn C.
Theo giả thiết ABCD là hình chữ nhật nên thể tích khối chóp S.ABCD là:
S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
Chọn C.
Ta có: SA ⊥ (ABCD)
ABCD là hình chữ nhật
S A B C D = A B . A D = a . 2 a = 2 a 2
Thể tích khối chóp S.ABCD là:
V S . A B C D = 1 3 S A B C D . S A = 1 3 2 a 2 . a 3 = 2 a 3 3 3
\(V_{SBCD}=\dfrac{1}{2}V_{SABCD}=\dfrac{1}{6}.SA.AB.AD=\dfrac{a^3\sqrt{3}}{3}\)
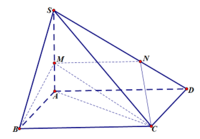
Đáp án D
Mặt phẳng ( M B C ) ∩ ( S A D ) = M N / / A D , M N / / B C
Gọi V 1 , V 2 lần lượt là thể tích khối S.MBCN và MN.ABCD
Ta có: V S . A B C = V S . A C D = 1 2 . V S . A B C D
⇒ V S . M B C = 2 a - x 2 a . V S . A B C
Theo giả thuyết V 2 = V 1 ⇔ V 1 = 1 2 V S . A B C D
Do đó 2 a - x 2 a + 2 a - x 2 a 2 = 1