Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
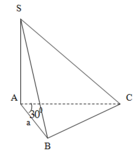
B C = A B . tan 30 0 = a 3 3 ⇒ A C = a 2 3 + a 2 = 2 3 3 a V = 1 3 . S A . 1 2 . A B . B C = 1 3 . S A . 1 2 . a . a 3 3 = a 3 3 36 ⇒ S A = a 2 S B = a 2 4 + a 2 = a 5 2 V = 1 3 . d ( A ; S B C ) . 1 2 . S B . B C = 1 3 . d . 1 2 . a 5 2 . a 3 3 = a 3 3 36 ⇒ d = a 5 5

Đáp án A
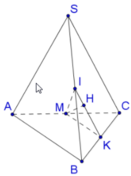
Gọi K là trung điểm của BC.
Do SAB ^ = SCB ^ = 90 o nên dễ dàng nhận thấy trung điểm I của SB là tâm mặt cầu ngoại tiếp chóp SABC.
Gọi M là trung điểm của AC.
Tam giác ABC vuông tại B, ta có MA = MB = MC , mặt khác IA = IB = IC , do đó IM là trục của đường tròn ngoại tiếp tam giác ABC hay IM ⊥ ABC



Đáp án D
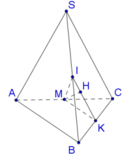
Gọi K là trung điểm của BC.
![]() nên dễ dàng nhận thấy trung điểm I của SB là tâm mặt cầu ngoại tiếp chóp SABC.
nên dễ dàng nhận thấy trung điểm I của SB là tâm mặt cầu ngoại tiếp chóp SABC.
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, ta có MA = MB = MC.
mặt khác IA = IB = IC, do đó IM là trục của đường tròn ngoại tiếp tam giác ABC hay IM ⊥ (ABC)

Xét tam giác vuông IMA ta có
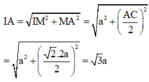
Vậy diện tích mặt cầu ngoại tiếp chóp SABC là
![]()

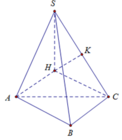
Đáp án B
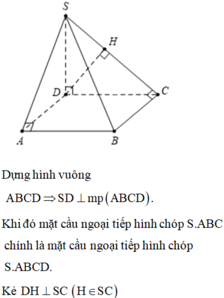
Dựng hình vuông ABCH
Ta có: A B ⊥ A H A B ⊥ S A ⇒ A B ⊥ S H , tương tự B C ⊥ S H
Do đó S H ⊥ A B C
Lại có A H / / B C ⇒ d A ; S B C = d H ; S B C
Dựng H K ⊥ S C ⇒ d H ; S B C − H K = a 2
Do đó 1 S H 2 = 1 H K 2 − 1 H C 2 ⇒ S H = a 6 .
Tứ giác ABCH nội tiếp nên R S . A B C = R S . A B C H = S H 2 4 + r 2 d
= S H 2 4 + A C 2 2 = a 3 ⇒ S = 4 π R 2 = 12 π a 2 .

Đáp án C
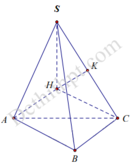
Dựng hình vuông ABCH
Ta có A B ⊥ A H A B ⊥ S A ⇒ A B ⊥ S H , tương tự B C ⊥ S H
Do đó S H ⊥ A B C
Lại có A H / / B C ⇒ d A ; S B C = d H ; S B C
Dựng H K ⊥ S C ⇒ d H ; S B C = H K = a 2
Do đó 1 S H 2 = 1 H K 2 − 1 H C 2 ⇒ S H = a 30 5
Tứ giác ABCH nội tiếp nên R S . A B C = R S . A B C H = S H 2 4 + r d 2
= S H 2 4 + A C 2 2 = a 2 ⇒ S = 4 π R 2 = 8 π a 2
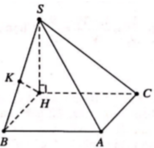


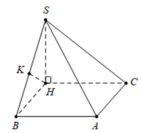


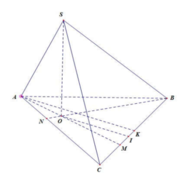

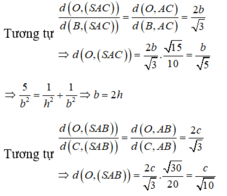
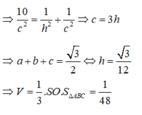

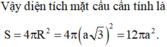
Đáp án D
Phương pháp:
Dựa vào công thức tính thể tích khối chóp
V = 1 3 S . h để suy ra chiều cao hạ từ C đến mp (SAB).
Cách giải:
Gọi khoảng cách từ C đến (SAB) là h.
Theo công thức thể tích khối chóp, ta có:
V = 1 3 h . S S A B = 1 3 . h .2 a 2 = a 3 3 → h = a 2
Chú ý khi giải:
HS cần áp dụng đúng công thức tính thể tích.