Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
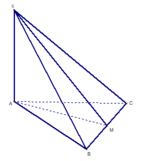
Gọi M là trung điểm của BC . Vì Δ A B C cân tại A nên A M ⊥ B C ,
Ta có A M ⊥ B C S M ⊥ B C S B C ∩ A B C = B C ⇒ Góc giữa S B C và A B C là góc Vì góc S A M = 90 0
Có B M = a , góc B A M = 60 0 nên
sin B A M = B M A B ⇒ A B = 2 a 3 ⇒ S Δ A B C = 1 2 A B . A C . sin 120 0 = a 2 3 3
tan B A M = B M A M ⇒ A M = a 3 ⇒ tan S M A = S A A M ⇒ S A = a 3
V S . A B C D = 1 3 . a 3 . a 2 3 3 = a 3 9

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)

Ta có: \(\widehat{A}=\frac{q}{3}\widehat{C}\).
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+80^o+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+\widehat{C}=180^o-80^o=100^o\)
=> \(\widehat{C}\left(q+3\right)=300^o\)
=> \(\widehat{C}=\frac{300^o}{q+3}\)
=> \(\widehat{A}=\frac{q}{3}.\frac{300^o}{q+3}=\frac{100^oq}{q+3}\)

a: \(\text{Δ}ABC\sim\text{Δ}HBA;\text{Δ}ABC\sim\text{Δ}HCA\)
b: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
CH=BC-BH=25-9=16(cm)

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)
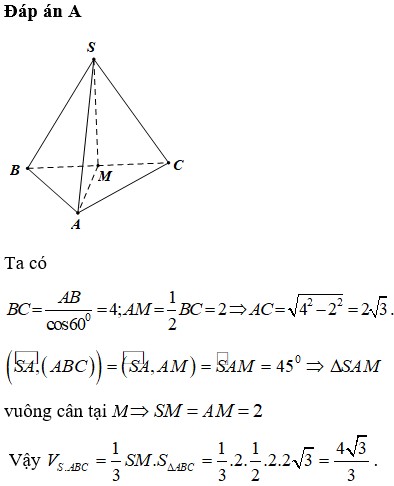

Đáp án B
Gọi M là trung điểm của BC . Vì Δ A B C cân tại A nên A M ⊥ B C ,
Ta có A M ⊥ B C S M ⊥ B C S B C ∩ A B C = B C
->Góc giữa S B C và A B C là góc S M A Vì góc S A M = 90 0
Có B M = a , góc B A M = 60 0 nên
sin B A M = B M A B ⇒ A B = 2 a 3 ⇒ S Δ A B C = 1 2 A B . A C . sin 120 0 = a 2 3 3
tan B A M = B M A M ⇒ A M = a 3 ⇒ tan S M A = S A A M ⇒ S A = a 3
V S . A B C D = 1 3 . a 3 . a 2 3 3 = a 3 9