Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 14: cho khoảng A = ( -∞ ; 6 / 2-m ) và khoảng B=(1-m ; + ∞ ) tìm tất cả các số thực để A \ B = A

ĐKXĐ: m<>2
Để A\B=A thì A giao B=rỗng
Để \(A\cap B=\varnothing\) thì \(\dfrac{6}{2-m}< =1-m\)
=>\(\dfrac{6-\left(1-m\right)\left(2-m\right)}{2-m}< =0\)
=>\(\dfrac{6-\left(m-2\right)\left(m-1\right)}{m-2}>=0\)
=>\(\dfrac{6-m^2+3m-2}{m-2}>=0\)
=>\(\dfrac{-m^2+3m+4}{m-2}>=0\)
=>\(\dfrac{m^2-3m-4}{m-2}< =0\)
=>\(\dfrac{\left(m-4\right)\left(m+1\right)}{m-2}< =0\)
Đặt \(F\left(x\right)=\dfrac{\left(m-4\right)\left(m+1\right)}{m-2}\)
Đặt m-4=0
=>m=4
Đặt m+1=0
=>m=-1
Đặt m-2=0
=>m=2
Ta có bảng xét dấu:
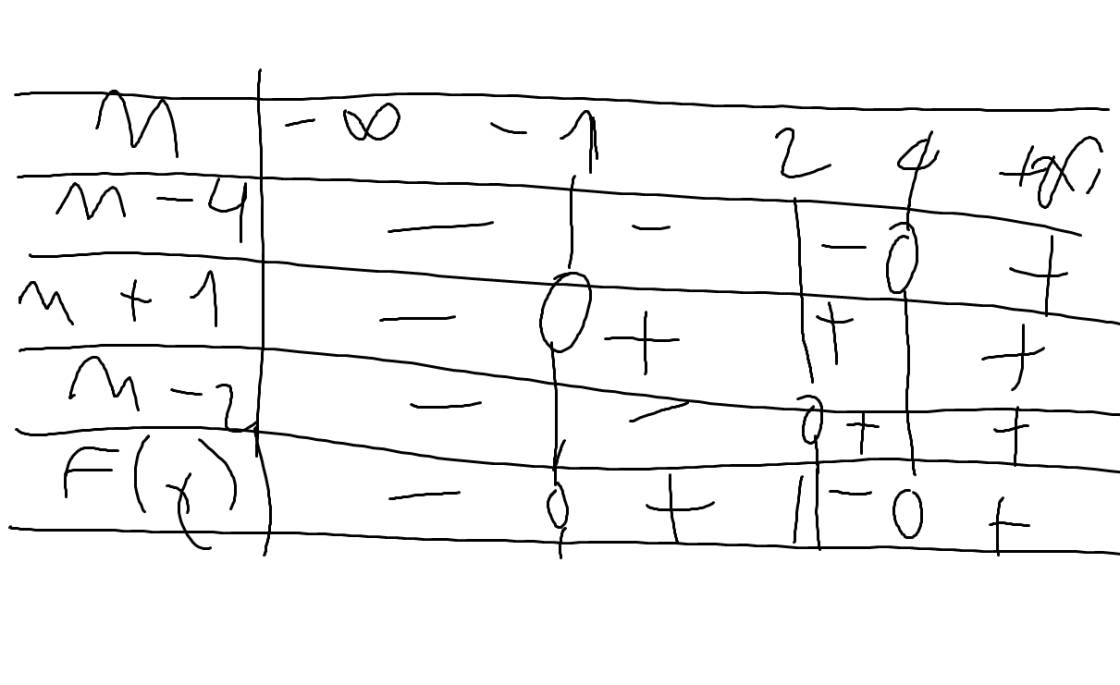
Theo BXD, ta có:F(x)<=0
=>\(\left[{}\begin{matrix}m< =-1\\2< m< =4\end{matrix}\right.\)

Điều kiện để A xác định là:
\(m-1< 8\)
\(\Leftrightarrow m< 8+1\Leftrightarrow m< 9\)
Để: \(A\backslash B=\varnothing\)
\(\Leftrightarrow A\subset B\) \(\Rightarrow2\le m-1\)
\(\Leftrightarrow m\ge3\)
kết hợp với điều kiện:
\(\Rightarrow3\le m< 9\)

Để A giao B khác rỗng thì \(7-4m< =4-m\)
=>-3m<=-3
=>m>=1
=>Chọn A



Để A \ B = A thid 5 - 4m < 2 - m
⇔-4m + m < 2 - 5
⇔ -3m < -3
⇔ m > 1
Vậy m > 1 thì A \ B = A