Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác ACB, có CO là trung tuyến. Lại có \(CO=OA=OB=\frac{AB}{2}\), vậy nên tam giác ACB vuông lại C.
b) Xét tam giác vuông ACB, ta có:
\(\sin\widehat{CAB}=\frac{BC}{BA}=\frac{1}{2}\Rightarrow\widehat{CAB}=30^o\)
Xét tam giác vuông ACB, ta có:
\(cos\widehat{CAB}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}\Rightarrow AC=R\sqrt{3}\)
Xét tam giác vuông ABD, ta có:
\(\tan\widehat{DAB}=\frac{BD}{AB}=\frac{\sqrt{3}}{3}\Rightarrow BD=\frac{2\sqrt{3}R}{3}\)
c) Ta thấy ngay tam giác BCD vuông tại C nên tâm đường tròn ngoại tiếp tam giác BCD là trung điểm cạnh huyền.
Vậy O' là trung điểm BD.
Xét tam giác OCO' và OBO' có:
O'C = O'B (gt)
OC = OB (= R)
OO' chung
\(\Rightarrow\Delta OCO'=\Delta OBO'\left(c-c-c\right)\)
\(\Rightarrow\widehat{O'CO}=\widehat{OBO'}=90^o\)
Vậy nên O'C là tiếp tuyến của đường tròn (O).
Lại có AB vuông góc với O'B tại B nên AB là tiếp tuyến tại B của đường tròn (O').
d) Gọi H là hình chiếu của I trên OB.
\(AD=\sqrt{AB^2+BD^2}=\frac{4R\sqrt{3}}{3}\)
Ta có hai công thức tính diện tích tam giác:
Công thức Hê-rông: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) với a, b, c là độ dài các cạnh của tam giác, p là nửa chu vi
\(S=pr\) với r bán kính đường tròn nội tiếp.
Vậy nên \(r=\sqrt{\frac{\left(p-AB\right)\left(p-BD\right)\left(p-AD\right)}{p}}\)
\(p=\frac{AD+DB+BA}{2}=\left(1+\sqrt{3}\right)R\)
Vậy thì:
\(r=R\sqrt{\frac{4-2\sqrt{3}}{3}}=\frac{3-\sqrt{3}}{3}R\)
Thấy ngay IH = r.
Xét tam giác HIB có góc H vuông, \(\widehat{IBH}=45^o\) (Do BI là phân giác góc vuông)
Vậy nên \(IH=HB=\frac{3-\sqrt{3}}{3}R\)
\(\Rightarrow OH=R-HB=\frac{R\sqrt{3}}{3}\)
Xét tam giác vuông OIH, ta có:
\(OI=\sqrt{OH^2+IH^2}=R\sqrt{\frac{5-2\sqrt{3}}{3}}\)

a) Xét tam giác ACB, có CO là trung tuyến. Lại có \(CO=OA=OB=\frac{AB}{2}\), vậy nên tam giác ACB vuông lại C.
b) Xét tam giác vuông ACB, ta có:
\(\sin\widehat{CAB}=\frac{BC}{BA}=\frac{1}{2}\Rightarrow\widehat{CAB}=30^o\)
Xét tam giác vuông ACB, ta có:
\(cos\widehat{CAB}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}\Rightarrow AC=R\sqrt{3}\)
Xét tam giác vuông ABD, ta có:
\(\tan\widehat{DAB}=\frac{BD}{AB}=\frac{\sqrt{3}}{3}\Rightarrow BD=\frac{2\sqrt{3}R}{3}\)
c) Ta thấy ngay tam giác BCD vuông tại C nên tâm đường tròn ngoại tiếp tam giác BCD là trung điểm cạnh huyền.
Vậy O' là trung điểm BD.
Xét tam giác OCO' và OBO' có:
O'C = O'B (gt)
OC = OB (= R)
OO' chung
\(\Rightarrow\Delta OCO'=\Delta OBO'\left(c-c-c\right)\)
\(\Rightarrow\widehat{O'CO}=\widehat{OBO'}=90^o\)
Vậy nên O'C là tiếp tuyến của đường tròn (O).
Lại có AB vuông góc với O'B tại B nên AB là tiếp tuyến tại B của đường tròn (O').
d) Gọi H là hình chiếu của I trên OB.
\(AD=\sqrt{AB^2+BD^2}=\frac{4R\sqrt{3}}{3}\)
Ta có hai công thức tính diện tích tam giác:
Công thức Hê-rông: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) với a, b, c là độ dài các cạnh của tam giác, p là nửa chu vi
\(S=pr\) với r bán kính đường tròn nội tiếp.
Vậy nên \(r=\sqrt{\frac{\left(p-AB\right)\left(p-BD\right)\left(p-AD\right)}{p}}\)
\(p=\frac{AD+DB+BA}{2}=\left(1+\sqrt{3}\right)R\)
Vậy thì:
\(r=R\sqrt{\frac{4-2\sqrt{3}}{3}}=\frac{3-\sqrt{3}}{3}R\)
Thấy ngay IH = r.
Xét tam giác HIB có góc H vuông, \(\widehat{IBH}=45^o\) (Do BI là phân giác góc vuông)
Vậy nên \(IH=HB=\frac{3-\sqrt{3}}{3}R\)
\(\Rightarrow OH=R-HB=\frac{R\sqrt{3}}{3}\)
Xét tam giác vuông OIH, ta có:
\(OI=\sqrt{OH^2+IH^2}=R\sqrt{\frac{5-2\sqrt{3}}{3}}\)

Đáp án B
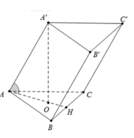
Ta có: S đ = a 2 3 4 ; O A = 2 3 A H = a 3 3
Mặt khác AA' hợp với đáy ABC một góc 60 ∘
nên A ' O H ⏜ = 60 ∘ suy ra A ' H = O A tan 60 ∘ = a .
Suy ra V A B C . A ' B ' C ' = S đ h = a 3 3 4

Xét (O) có
ΔCDM nội tiếp
CM là đường kính
DO đó: ΔCDM vuông tại D
Xét tứ giác ABCD có
\(\widehat{CDB}=\widehat{CAB}=90^0\)
Do đó: ABCD là tứ giác nội tiếp
b: \(\widehat{BCA}=\widehat{ADB}\)
mà \(\widehat{ADB}=\widehat{KCA}\)
nên \(\widehat{BCA}=\widehat{KCA}\)
hay CA là tia phân giác của góc KCB

Làm trên này là fai có cáh giải nuk cháu ak, ghi kq chỉ tổ tốn côg

