Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

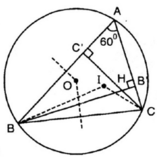

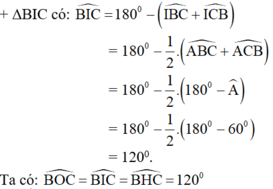
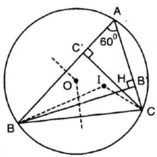
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.
Kiến thức áp dụng
+ Các điểm cùng nhìn một đoạn thẳng cố định dưới cùng một góc α thì đều thuộc cùng một đường tròn.


![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
![]()
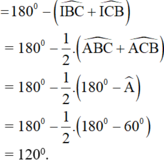
![]()
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.

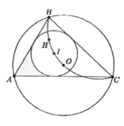
Chứng minh được B I C ^ = 120 0
=> B O C ^ = 2 B A C ^ = 120 0 => B H C ^ = 180 0 - 60 0 = 120 0 (góc nội tiếp và góc ở tâm)
=> H, I, O cùng nhìn BC dưới góc 120 0 nên B, C, O, I, H cùng thuộc một đường tròn

A B C O I A' B' C' E F D G S
a) Ta có ^AIC' = ^IAC + ^ICA = ^IAB + ^ICB = ^IAB + ^BAC' = ^IAC' => \(\Delta\)AC'I cân tại C'
=> C' nằm trên trung trực của AI. Tương tự B' cũng nằm trên trung trực của AI => B'C' vuông góc AI
Hay A'I vuông góc với B'C'. Lập luận tương tự B'I vuông góc A'C', C'I vuông góc A'B'
Do đó I là trực tâm của \(\Delta\)A'B'C' (đpcm).
b) Ta thấy ^FDE = ^A'DC' = ^A'AC' = ^IAC' = C'IA (Vì \(\Delta\)AC'I cân tại C') = ^EIC'
Suy ra tứ giác DEIF nội tiếp (đpcm).
c) Gọi S là tâm ngoại tiếp của \(\Delta\)DEF. Vì tứ giác DEIF nội tiếp (cmt) nên S đồng thời là tâm ngoại tiếp DEIF
Gọi giao điểm thứ hai giữa (S) và (O) là G. Khi đó ^DFG = ^DEG => ^GFA' = ^GEC'
Lại có ^EGF = ^EDF = ^A'DC' = ^A'GC' => ^FGA' = ^EGC'. Do vậy \(\Delta\)GEC' ~ \(\Delta\)GFA' (g.g)
=> \(\frac{GC'}{GA'}=\frac{EC'}{FA'}\). Mặt khác ^A'IF = ^C'IA = ^C'AI = ^C'AE và ^IA'F = ^AA'D = ^AC'D = ^AC'E
Cho nên \(\Delta\)AEC' ~ \(\Delta\)IFA' (g.g) => \(\frac{EC'}{FA'}=\frac{AC'}{IA'}\). Mà các điểm A,I,A',C' đều cố định
Nên tỉ số \(\frac{AC'}{FA'}\) là bất biến. Như vậy \(\frac{GC'}{GA'}\)không đổi, khi đó tỉ số giữa (GC' và (GA' của (O) không đổi
Kết hợp với (O), A',C' cố định suy ra G là điểm cố định. Theo đó trung trực của IG cố định
Mà S thuộc trung trực của IG (do D,I,E,F,G cùng thuộc (S)) nên S di động trên trung trực của IG cố định (đpcm).

A B C O M N E K T
a) Có ^AOB = 1800 - ^OAB - ^OBA = 1800 - ^BAC/2 - ^ABC/2 = 900 + (1800 - ^BAC - ^ABC)/2 = 900 + ^ACB/2
b) Dễ thấy A,M,O,E cùng thuộc đường tròn đường kính OA (Vì ^AMO = ^AEO = 900) (1)
Ta có ^AOK = 1800 - ^AOB = 1800 - (900 + ^ABC/2) = 900 - ^ACB/2 = ^CEN (Do \(\Delta\)CEN cân tại C)
=> Tứ giác AOKE nội tiếp hay A,O,K,E cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra năm điểm A,M,K,O,E cùng thuộc một đường tròn (đpcm).
c) Ta thấy A,O,K,E cùng thuộc một đường tròn (cmt) và OK cắt AE tại T
Nên \(\frac{KT}{ET}=\frac{AT}{OT}\)(Hệ thức lượng đường tròn). Kết hợp \(\frac{AT}{OT}=\frac{AB}{OB}\)(AO là phân giác ^BAT)
Suy ra \(\frac{KT}{ET}=\frac{AB}{OB}\). Mặt khác: ^BKN = ^OAE = ^BAO và ^NBK = ^OBA => \(\Delta\)BKN ~ \(\Delta\)BAO (g.g)
=> \(\frac{AB}{OB}=\frac{KB}{NB}\). Từ đây \(\frac{KT}{ET}=\frac{KB}{BN}\)=> KT.BN = KB.ET (đpcm).

Câu hỏi của Lê Thanh Bình - Toán lớp 9 - Học toán với OnlineMath
bạn tham khảo

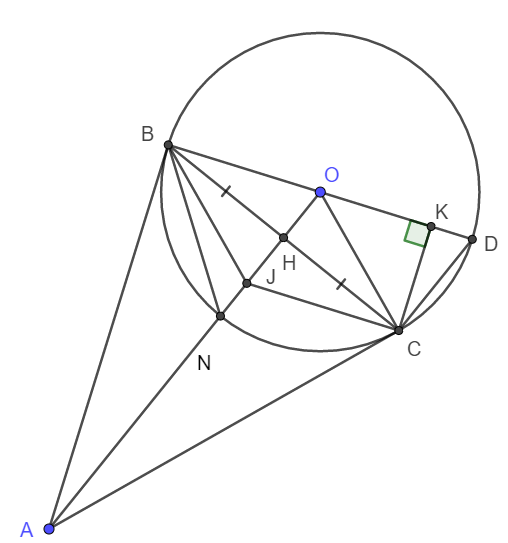
a) Tam giác vuông ABO và ACO có chung cạnh huyền AO nên O, B, A, C cùng thuộc đường tròn đường kính AO.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có AB = AC nên ABC là tam giác cân tại A.
Lại có AO là phân giác nên đồng thời là đường trung tuyến. Vậy thì AO đi qua H hay A, H, O thảng hàng.
Theo liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung, ta có \(\widehat{KDC}=\frac{\widehat{BOC}}{2}\)
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có: \(\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Suy ra \(\widehat{KDC}=\widehat{COA}\)
Vậy thì \(\Delta KDC\sim\Delta COA\left(g-g\right)\Rightarrow\frac{CK}{AC}=\frac{CD}{AO}\Rightarrow AC.CD=CK.AO\)
c) Ta thấy \(\widehat{ABN}=\widehat{NBC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung chắn các cung bằng nhau)
Vậy nên BN là phân giác góc ABC.
Lại có AN là phân giác góc BAC nên N là tâm đường tròn nội tiếp tam giác ABC.
d) Gọi J là trực tâm tam giác ABC. Ta có ngay \(JC\perp AB;BJ\perp AC\)
Vậy thì BO // JC ; BJ // OC
Suy ra tứ giác JBOC là hình bình hành.
Lại có OB = OC nên JBOC là hình thoi.
Từ đó ta có JB = JC = OB = OC = R.
Vậy khi A di chuyển trên tia By cố định thì BJ = R hay J thuộc đường tròn tâm B, bán kính R.
Ta có: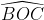 = 2
= 2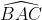 = 2.60o = 120o (1)
= 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và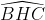 =
= 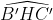 (đối đỉnh)
(đối đỉnh)
mà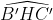 = 180o -
= 180o - 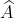 = 180o - 60o = 120o
= 180o - 60o = 120o
nên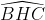 = 120o (2)
= 120o (2)
= 60o +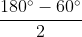 = 60o+ 60o
= 60o+ 60o
(sử dụng góc ngoài của tam giác)
Do đó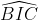 = 120o
= 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn
Ta có: \(\widehat{BOC}\) = 2\(\widehat{BAC}\) = 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và \(\widehat{BHC}\) = \(\widehat{B'HC'}\) (đối đỉnh)
mà \(\widehat{B'HC'}\) = 180o - \(\widehat{A}\) = 180o - 60o = 120o
nên \(\widehat{BHC}\) = 120o (2)
\(\widehat{BIC}\) = \(\widehat{A}\) + \(\dfrac{\widehat{B}+\widehat{C}}{2}\)
= 60o + \(\dfrac{180^0-60^0}{2}\) = 60o+ 60o
(sử dụng góc ngoài của tam giác)
Do đó \(\widehat{BIC}\) = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn