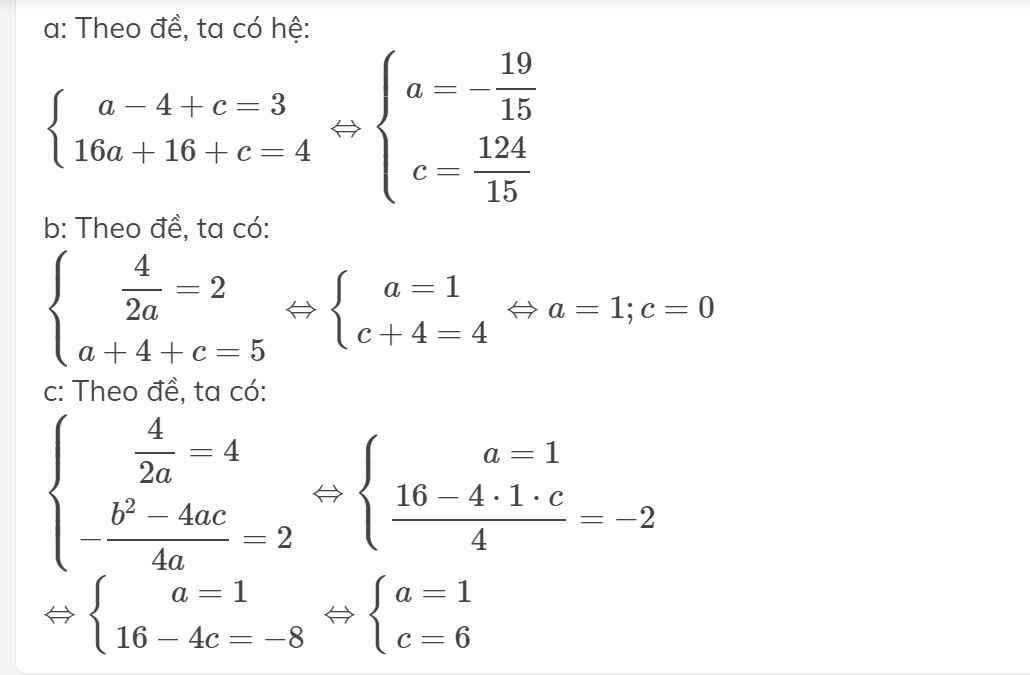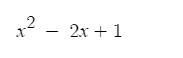Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-4x+1=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+5=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-5\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(1;-2\right);\left(5;6\right)\right\}\)
c: Điểm M,N ở đâu vậy bạn?

Khảo sát &vẽ chịu
với giá trị nào ...y=mx+m-1
Phương trình: x^2-4x+3=mx+m-1 phải có 2 nghiệm
\(\Leftrightarrow x^2-\left(m+4\right)x+3-m+1=0\) \(\Delta_x=\left(m+4\right)^2-4\left(4-m\right)>0\)
\(\left(m+4\right)^2+4\left(m+4\right)-32>0\)(*)
\(\Delta'_{m+4}=4+32=36\) Nghiệm (pt) (*) là \(\left[\begin{matrix}\left(m+4\right)=-2-6=-8\\\left(m+4\right)=-2+6=4\end{matrix}\right.\)
Nghiệm BPT(*) \(\Leftrightarrow-8< \left(m+4\right)< 4\Leftrightarrow-12< m< 0\)
Kết luận: Với \(-12< m< 0\) thì...cắt nhau tại hai điểm phân biệt.

a: \(\left\{{}\begin{matrix}x_I=\dfrac{3}{2\cdot1}=\dfrac{3}{2}\\y_I=-\dfrac{\left(-3\right)^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{17}{4}\end{matrix}\right.\)

Ta có: \(y=x^2-2x+1\), có: \(a=1>0;b=-2;c=1\)
+ Tập xác định: \(D=R\)
+ Nghịch biến trên: \(\left(-\infty;1\right)\); đồng biến trên \(\left(1;+\infty\right)\)
Bảng biến nhiên:
| x | \(-\infty\) 1 \(+\infty\) |
| y | \(+\infty\) → 0 → \(-\infty\) |
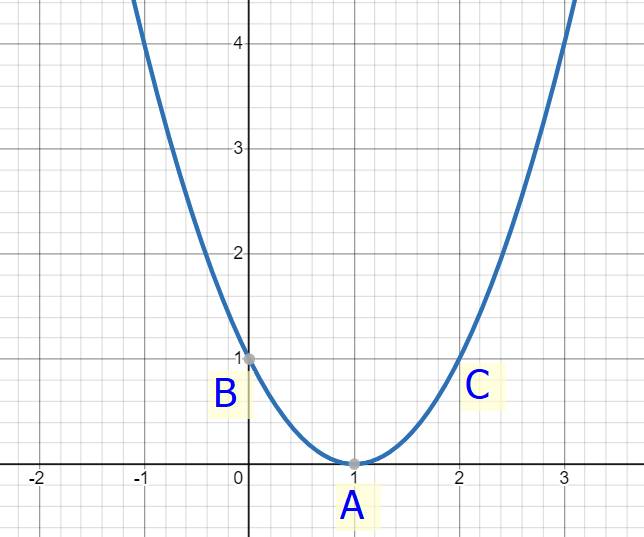
+ Đồ thị hàm số parabol có:
Đỉnh: \(A\left(1;0\right)\)
Trục đối xứng là đường thẳng x = 1
Giao điểm với Oy tại \(B\left(0;1\right)\), điểm đối xứng với B qua đường thẳng x = 1 là \(C\left(2;1\right)\)
Đi qua các điểm \(\left(-1;4\right);\left(3;4\right)\)

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2