Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

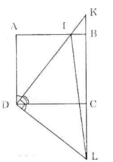
a) Xét hai tam giác vuông ADI và CDL có:
AD = CD (cạnh hình vuông)
![]()
Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)
Suy ra DI = DL hay ΔDIL cân. (đpcm)
b) Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:
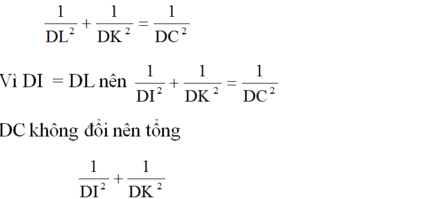
không đổi khi I thay đổi trên cạnh AB. (đpcm)

Bài 2)
1) xét tứ giác AEHF có góc A=90* F=90* E=90* (GT)
==)) AEHF Là hình chữ nhật
2) Vì AEHF là hình chữ nhật ==)) EF=AH(đl) gọi O là giao điểm của EF và AH
==))EO=OF=AO=OH
EO=AO ==)) tam giác EOA cân tại O,==)) OEA=góc OAE
mà góc OAE=góc BCA (cùng phụ với góc HAC ) ==))góc OEA =góc BCA(1)
góc A=90* chung ==)) tam giác EAF~tam giác CAB (g-g)
==))EA/CA=AF/AB ==))AE.AB=AF.AC
2)ta có BH.HC=AH2
AH2=( AO+OH )2=AO2+OH2+2AO.OH mà AO=OH ==))AH2=4.OA2
4EO.OF=4OE2 mà OE=OA(cmt)==))4EO.OF=AH2=BH.HC

Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:
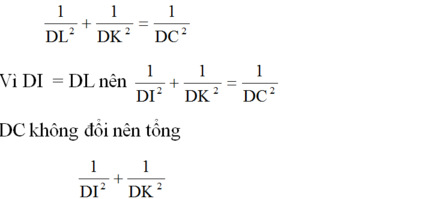
không đổi khi I thay đổi trên cạnh AB. (đpcm)

Xét Tam giác ADI vuông tại A và tam giác CDL vuông tại C có :
AD = DC ( ABCD là HV)
ADI = CDL ( cùng phụ KDC )
=> Tam giác ADI = CDL ( c.g.v - g.n.k )
=> DI = DL => tam giác DIL cân tại I
b)
TAm giác DCL vuông tại D , theo HTL ;
\(\frac{1}{DC^2}=\frac{1}{DK^2}+\frac{1}{DL^2}\)
DI = DL => \(\frac{1}{DC^2}=\frac{1}{DK^2}+\frac{1}{DI^2}\)
Vì DC không đổi => \(\frac{1}{DC^2}\) ko đổi
=> \(\frac{1}{DK^2}+\frac{1}{DI^2}\) ko đổi
Xét tam giác ADI vuông tại A và tam giác CDL vuông tại C có :
AD = DC ( ABCD la HV )
ADI = CDL ( cung phụ KDC )
\(\Rightarrow\) Tam giác ADI = CDL ( c . g . v - g . n . k )
\(\Rightarrow\)DI = DL \(\Rightarrow\) tam giác DIL cân tại I
b,
Tam giác DCL vuông tại D , theo HTL
\(\frac{1}{DC^2}\) = \(\frac{1}{DK^2}\) +\(\frac{1}{DL^2}\)
DI = DL => \(\frac{1}{DC^2}\) = \(\frac{1}{DK^2}\) + \(\frac{1}{DI^2}\)
Vì DC không đổi => \(\frac{1}{DC^2}\) không đổi
=> \(\frac{1}{DK^2}\) + \(\frac{1}{DI^2}\) không đổi