Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GỢI Ý
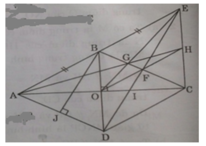
Bạn tự vẽ hình.
1) Gọi độ dài cạnh của hình vuông ABCD là a (\(AB=BC=CD=DA=a\))
△DCF∼△BEC (g-g) \(\Rightarrow\dfrac{DF}{a}=\dfrac{a}{BE}\)
BE//CD \(\Rightarrow\dfrac{a}{BE}=\dfrac{CH}{BH}\)
DF//BC \(\Rightarrow\dfrac{DF}{a}=\dfrac{DG}{CG}\)
\(\Rightarrow\dfrac{DG}{CG}=\dfrac{CH}{BH}\Rightarrow\dfrac{DG}{CH}=\dfrac{CG}{BH}=\dfrac{DG+CG}{CH+BH}=\dfrac{DC}{BC}=1\)
\(\Rightarrow DG=CH;CG=BH\)
△ADE∼△CHD \(\Rightarrow\dfrac{a}{AE}=\dfrac{CH}{a}\left(1\right)\)
△BCG∼△FAB \(\Rightarrow\dfrac{a}{AF}=\dfrac{CG}{a}\left(2\right)\)
\(\left(1\right)+\left(2\right)\Rightarrow a\left(\dfrac{1}{AE}+\dfrac{1}{AF}\right)=\dfrac{CH+CG}{a}=\dfrac{CH+BH}{a}=1\)
\(\Rightarrow\dfrac{AC}{AE}+\dfrac{AC}{AF}=\sqrt{2}\)
b) BỔ ĐỀ HÌNH THANG: Trong hình thang, đường thẳng tạo bởi giao điểm của hai đường chéo và giao điểm của hai cạnh bên thì đi qua 2 trung điểm của hai đáy.
Quay lại bài toán:
Qua O kẻ đường thẳng // với AF cắt AB, CF tại X,Y.
*Chứng minh OX=OY (dùng định lí Thales giới hạn trong các tam giác trong hình thang ABCF).
*Chứng minh K là trung điểm AF (dùng định lí Thales trong các tam giác AKE, FKE).

b) Xét Δ BCD có: O là trung điểm của BD
F là trung điểm của BC
⇒ OF là đường trung bình của ΔBDC ⇒ OF // DC mà DC // AB nên OF // AE
⇒ FH // BE
Mà O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của ΔAEC. Mà AH cắt EO tại G nên G là trong tâm của ΔAEC ⇒ A, G, H thẳng hàng.

A B C D E F O
có hình thoi ABCD (gt) => AB = BC (Đn)
có : AB = AC (gt)
=> AB = BC = AC
=> tam giác ABC đều (đn)
=> ^ABC = 60 (tc)
có : BC // AD do ABCD là hình thoi (gt) ; ^ABC slt ^EAB
=> ^EAB = 60 (tc)
tương tự => ^EAB = ^BCF = 60
có : AD // BC (cmt) => ^AEB = ^CBF (đv)
xét tam giác AEB và tam giác CBF
=> tam giác AEB đồng dạng với tg CBF (g-g)
=> AE/AB = BC/CF (đn)
có : AB = BC = AC (cmt)
=> AE/AC = AC/CF
có : ^EAC = ^ACF = 120 (tự cm)
xét tam giác EAC và tam giác ACF
=> tam giác EAC đồng dạng với tg ACF (c-g-c)
=> ^AEC = ^OAC (Đn)
xét tam giác EAC và tg AOC có : ^ACO chung
=> tg EAC đồng dạng với tg AOC (g-g)
=> ^AOC = ^EAC (đn) mà ^EAC = 120
=> ^AOC = 120 có : ^AOC = ^EOF (đối đỉnh)
=> ^EOF = 120

