Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Độ dài đoạn thẳng BM là:
12 * 2/3 = 8 ( cm )
Diện tích hình tam giác ABM là:
12 * 8 / 2 = 48 ( cm2)
b) thấy sai sai ở đâu đó kìa
Đề bài nhầm vi M thuộc BC nên AM kéo dài phải cắt CD tại K mới đúng
Xét tam giác ABC và tam giác ABM có chung đường cao hạ từ A xuống AB ( chính là AB) nên
\(\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{2}{3}\Rightarrow S_{ABM}=\frac{2xS_{ABC}}{3}=\frac{2xABxAC}{2x3}=\frac{12x12}{3}=48cm^2\)
Xét tam giác ABC và tam giác ABK có đường cao hạ từ C xuống AB bằng đường cao hạ từ K xuống AB nên
\(\frac{S_{ABC}}{S_{ABK}}=\frac{AB}{AB}=1\Rightarrow S_{ABK}=S_{ABC}=\frac{ABxAC}{2}=\frac{12x12}{2}=72cm^2\)
\(S_{BKM}=S_{ABK}-S_{ABM}=72-48=24cm^2\)
Xét tam giác ABM và tam giác BKM có chung BM nên
S(BKM) / S(ABM) = đường cao hạ từ K xuống BC / đường cao hạ từ A xuống BC = 24/48=1/2
\(S_{ACM}=S_{ABC}-S_{ABM}=72-48=24cm^2\)
Xét tam giác ACM và tam giác CKM có chung đáy CM nên
S(CKM) / S(ACM) = đường cao hạ từ K xuống BC / đường cao hạ từ A xuống BC =1/2 => S(CKM) = S(ACM)/2=24/2=12 cm2
Xét tam giác BCD và tam giác MCD có cung đường cao hạ từ D xuống BC (chính là CD) nên
\(\frac{S_{MCD}}{S_{BCD}}=\frac{MC}{BC}=\frac{1}{3}\Rightarrow S_{MCD}=\frac{S_{BCD}}{3}=\frac{BCxCB}{2x3}=\frac{12x12}{6}=24cm^2\)
Xét tam giác MCD và tam giác CKM có chung đường cao hạ từ M xuống CD nên
\(\frac{S_{CKM}}{S_{MCD}}=\frac{CK}{CD}=\frac{12}{24}=\frac{1}{2}\) mà BC=CD nên \(\frac{CK}{CD}=\frac{CK}{BC}=\frac{1}{2}\)

Theo đề bài ABCD là hình chữ nhật.
\(\Rightarrow DC=AB=12\left(cm\right).\)
\(S_{\Delta MDN}=\dfrac{1}{2}\times DN\times BC.\\ =\dfrac{1}{2}\times\dfrac{2}{3}DC\times BC.\\ \Rightarrow S_{\Delta MDN}=\dfrac{1}{2}\times\dfrac{2}{3}\times12\times6=24\left(cm^2\right).\)

1)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)
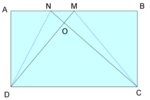
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)

Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC

nua chu vi là: 60 : 2= 30 cm
tong so phan bang nhau cua CD va CR la: 3 + 2 = 5
CR: 30 : 5 x 2= 12 cm
CD 30: 5 X 3= 18 cm
a, DTHCN: 12 x 18 = .........
b. Ve hình sẽ thấy
hai tam giác có cùng chieu cao là CE
canh BM = 2 MC nên DT.MBE = 2 DT .MCD
nua chu vi la :60:2=30(cm)
tong so phan bang nhau la :3+2=5
chieu dai la 30:5*3=18(cm)
chieu rong la :18*\(\frac{2}{3}\)=12(cm)
SABCD la: 12*18=216(cm2)
b, vi MB=2MC nen MEB=2MCD

Trả lời :
Bạn vào đây tham khảo nha , dài quá mk nhác viết :
https://olm.vn/hoi-dap/detail/10534222471.html
~ Study well ~
#)Giải :
a) Chiều dài hình chữ nhật ABCD là :
60 : 2 : ( 3 + 2 ) x 3 = 18 ( cm )
Chiều rộng hình chữ nhật ABCD là :
60 : 2 : ( 3 + 2 ) x 3 = 12 ( cm )
Diện tích hình chữ nhật ABCD là :
18 x 12 = 216 ( cm2)
b) Diện tích hình tam giác ABE là :
18 x 12 : 2 = 108 ( cm2)
Diện tích hình tam giác ABM là :
18 x ( 12 : 3 x 2 ) : 2 = 72 ( cm2)
Diện tích hình tam giác MBE là :
108 - 72 = 36 ( cm2)
Diện tích hình tam giác MCD là :
18 x ( 12 - 8 ) : 2 = 36 ( cm2)
Vậy diện tích tam giác MBE = diện tích tam giác MCD
a, S ABM=48 cm 2
b,CK<DK( vì CK+DC=DK)