Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

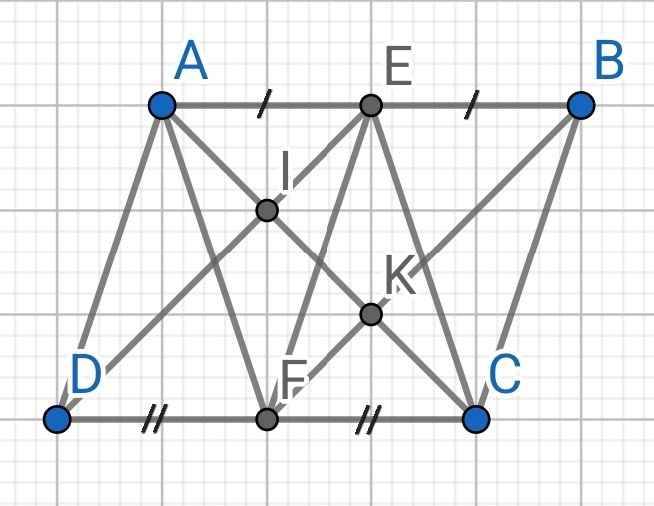 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC

a, xét tam giác IHE và tam giác BHA có :
góc IHE = góc BHA = 90
IH = HB do I đx B qua H (gt)
AH = HE do A đx E qua H (gT)
=> tam giác IHE = tam giác BHA (2cgv)
=> IE = AB (đn)
góc EIH = góc HBA (đn) mà 2 góc này slt => IE // AB (đl)
=> IEBA là hình bnhf hành (dh/9
AB _|_ AC (gt)
IE // AB (cmt)
=> IE _|_ AC (đl)


A B C D F K I E M
ta có gDAE + gEAB = 90 ( ABCD la hv)
gDAE +gDAF =90 (gt)
=> gEAB = gDAF
Xét tg ADF và tg ABE có gFAD = gBAE (cmt)
AD =AB ( ABCD la hv)
gADF = gABE =90
=> tg ADF = tg ABE (cgv-gnk) => AF = AE => tg AEF can tai A
b) tg AEF cân tại A có AI là đường trung tuyến ( I là trung điểm của EF)
=> AI đồng thời là đường cao (tc ) => AI vuông góc với EF hay KM vuông góc với EF
Xet tg KIE va tg MIF co gKIE = gEIM ( doi dinh )
IE =IF ( I là tđ cua EF)
gKEI =g IEM ( SLT do EK // CD)
=> tg KIE =tg MIF => IK =IM va KE =MF
Xet tu giac KEMF co IK=IM IE=IF ma MK cat EF tai I
=> tgiac KEMF la hbh mà KM vuông góc E tại I => tgiac KEMF la hinh thoi