Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài ta có :AM = 1/2 AD nên AM bằng 1/2 BC , Ta có :
sAMB = 1/2 sBMC hay sBMC = 2 nhân sAMB
b] sBMC =2nhân sAMB , mà hai tam giác chung đáy MB nên chiều cao CI gấp đôi chièu cao AH
Tam giác BNC và ANC có chung đáy NB , chiều cao CI = 2 nhân AH
Suy sBNC = 2 nhân sANB
sABC = 1/2 sABCD
sABC = 1,5 * ( 1 + 2) = 4,5 dm 2
sABCD =4,5 * 2= 9 dm2
sABCD = 4,5 * 2 = 9


a) Ta thấy tam giác BMC có đáy BC và chiều cao bằng AB
Tam giác AMB có đáy AM và chiều cao AB
Lại có BC = AD = 2AM nên diện tích tam giác BMC gấp 2 lần diện tích tam giác AMB.
b) Ta thấy tam giác BNC và tam giác BNA chung chiều cao nên \(\frac{S_{BNC}}{S_{BNA}}=\frac{NC}{AN}\)
Tam giác MCN và tam giác MAN chung chiều cao nên \(\frac{S_{MCN}}{S_{MAN}}=\frac{NC}{AN}\)
Vậy nên \(\frac{S_{ABC}}{S_{AMC}}=\frac{NC}{AN}\)
Mà ta thấy tam giác ABC và tam giác AMC có chiều cao bằng nhau, BC = 2AM nên \(\frac{S_{ABC}}{S_{AMC}}=2\Rightarrow\frac{NC}{AN}=2\)
Tam giác BNC và tam giác ANB có chung chiều cao nên \(\frac{S_{BNC}}{S_{ANB}}=\frac{NC}{AN}=2\)
Ta có \(\frac{S_{BNC}}{S_{ANB}}=2\Rightarrow\frac{S_{ABC}}{S_{ANB}}=3\Rightarrow\frac{S_{ABCD}}{S_{ANB}}=6\)
Vậy diện tích ABCD bằng: 1,5 x 6 = 9 (dm2)
Lời giải:
a.
$\frac{S_{DMC}}{S_{DMA}}=\frac{AD\times DC}{2}: \frac{AM\times AD}{2}=\frac{AD\times DC}{AM\times AD}=\frac{DC}{AM}=\frac{AB}{\frac{AB}{2}}=2$
Vậy diện tích tam giác DMC gấp 2 lần diện tích tam giác DMA
b.
Kẻ đường cao AH của tam giác $ADM$ và đường cao $CK$ của tam giác $DCM$
Ta có:
$2=\frac{S_{DCM}}{S_{DMA}}=\frac{CK\times MD}{2}: \frac{AH\times DM}{2}=\frac{CK}{AH}$
Suy ra:
$\frac{S_{ADN}}{S_{DNC}}=\frac{AH\times DN}{2}: \frac{CK\times DN}{2}=\frac{AH}{CK}=\frac{1}{2}$
$2\times S_{ADN}=\times S_{DNC}$
$3\times S_{ADN}=S_{DNC}+S_{ADN}=S_{ADC}=AD\times DC:2=S_{ABCD}:2$
$S_{ABCD}=3\times S_{ADN}\times 2=6\times S_{ADN}=6\times 5=30$ (cm2)
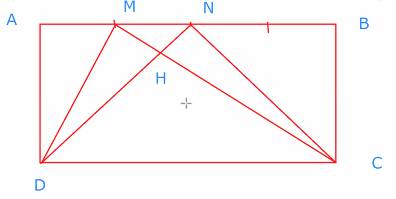
Hình vẽ: