Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCIF vuông tại I và ΔCBE vuông tại B có
góc bCE chung
=>ΔCIF đồng dạg với ΔCBE
b: ΔFCD vuông tại C có CI là đường cao
nên CI^2=FI*ID

a, Vì \(\left\{{}\begin{matrix}AD=AB\\AI=DK\left(\dfrac{1}{2}AD=\dfrac{1}{2}DC\right)\\\widehat{BAD}=\widehat{ADK}=90^0\end{matrix}\right.\) nên \(\Delta AIB=\Delta DKA\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{DAI}\\ \Rightarrow\widehat{DAI}+\widehat{AIB}=\widehat{ABI}+\widehat{AIB}=90^0\\ \Rightarrow BI\perp AK\)

1: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\)(1)
K là trung điểm của CD
=>\(DK=KC=\dfrac{DC}{2}\)(2)
ABCD là hình vuông
=>AB=DC(3)
Từ (1),(2),(3) suy ra AE=EB=CK=KD
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
2: Xét ΔFCD vuông tại C và ΔEBC vuông tại B có
FC=EB
CD=BC
Do đó: ΔFCD=ΔEBC
=>\(\widehat{FDC}=\widehat{ECB}\)
mà \(\widehat{FDC}+\widehat{DFC}=90^0\)(ΔDFC vuông tại C)
nên \(\widehat{ECB}+\widehat{DFC}=90^0\)
=>DF\(\perp\)CE tại M
3: AECK là hình bình hành
=>AK//CE
AK//CE
CE\(\perp\)DF
Do đó: AK\(\perp\)CE tại N
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
4: Xét ΔADM có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
mà AD=AB
nên AM=AB
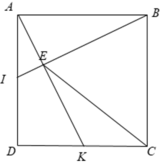

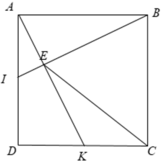




Ta có: \(AE=\dfrac{AB}{2}\)
\(CK=\dfrac{CD}{2}\)
mà AB=CD
nên AE=CK
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
=>CE//AK