Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
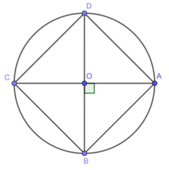
*Cách vẽ:
- Vẽ đường tròn tâm O bán kính 1,5cm
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB, BC , CD, DA lại với nhau ta được hình vuông ABCD nội tiếp trong đường tròn (O; 1,5)
*Chứng minh:
Ta có : OA = OC , OB =OD
Suy ra ABCD là hình bình hành
Mặt khác : AC = BD và AC ⊥ BD
Suy ra ABCD là hình vuông
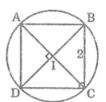
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng nằm trên một đường tròn
b: Tâm là trung điểm của AC
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
\(R=\dfrac{AC}{2}\)
bài này mình ra rồi nhé