Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Link ảnh: file:///C:/Users/THAOCAT/Pictures/Screenshots/Screenshot%20(1222).png
a) Gọi U là giao điểm của AD và BM
Dễ có: \(\widehat{ACB}=\widehat{ADB}=90^0\)(các góc nội tiếp chắn nửa đường tròn) hay \(\Delta ACU\)vuông tại C
và \(\Delta ABU\)cân tại B (có BD vừa là đường cao vừa là phân giác) => D là trung điểm của AU
\(\Delta ACU\)vuông tại C có CD là trung tuyến (cmt) nên CD = AD => \(\widehat{CAD}=\widehat{ABD}\)(góc nội tiếp chắn các cung bằng nhau)
b) \(\Delta ABU\)có ID là đường trung bình nên ID // BU hay IK // BM
\(\Delta ABM\)có I là trung điểm của AB, IK // BM nên K là trung điểm của AM
\(\Delta ACM\)vuông tại C có CK là trung tuyến nên \(CK=\frac{1}{2}AM\)(đpcm)
c) Ta có: \(AC+BC\le\sqrt{2\left(AC^2+BC^2\right)}=\sqrt{2AB^2}=2\sqrt{2}R\)
\(\Rightarrow AB+AC+BC\le\left(2\sqrt{2}+2\right)R\)
Vậy chu vi tam giác ABC lớn nhất bằng \(\left(2\sqrt{2}+2\right)R\)đạt được khi AC = BC hay AB = AM = 2R

a) Kẻ OP ⊥ AM, OQ ⊥ BN
Ta có: AM = BN (Giả thiết)
Suy ra: OP = OQ (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCP và OCQ, ta có:
Góc OPC= góc OQC=90∘
OC chung
OP = OQ (chứng minh trên)
Suy ra: ∆OCP = ∆OCQ (cạnh huyền, cạnh góc vuông)
Góc O1= góc O2
Xét hai tam giác OAP và OBQ, ta có:
Góc OPA= góc OQB=90∘
OA = OB
OP = OQ ( chứng minh trên)
Suy ra: ∆OAP = ∆OBQ (cạnh huyền, cạnh góc vuông)
Góc O3= Góc O4
Suy ra: Góc O1+góc O3= Góc O2+ góc O4 hay Góc AOC= Góc BOC
Vậy OC là tia phân giác của Góc AOB
b) Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân).
Suy ra: OC ⊥ AB.

O B A M N C E F
a) Do C là giao điểm của BN với đường tròn nên C thuộc đường tròn.
Lại có AB là đường kính nên \(\widehat{ACB}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
Vậy nên tam giác ABC vuông tại C.
b) Do M thuộc đường tròn nên \(\widehat{AMB}=90^o\Rightarrow EM\perp AN\)
Ta cũng có \(NC\perp AE\)
Xét tam giác ANE có EM, NC là các đường cao nên B là trực tâm.
Vậy thì \(AB\perp NE\)
c) Xét tứ giác AFNE có : MA = MN; MF = ME nên AFNE là hình bình hành (Dấu hiệu nhận biết)
\(\Rightarrow\) FN // AE
Ta chứng minh BA = BN và \(BN\perp FN\)
Thật vậy, xét tam giác ABN có MA = MN, \(BM\perp AN\) nên ABN là tam giác cân.
Vậy BA = BN
Ta có \(NC\perp AE\Rightarrow NC\perp FN\)
Suy ra NF là tiếp tuyến của đường tròn (B; BA).

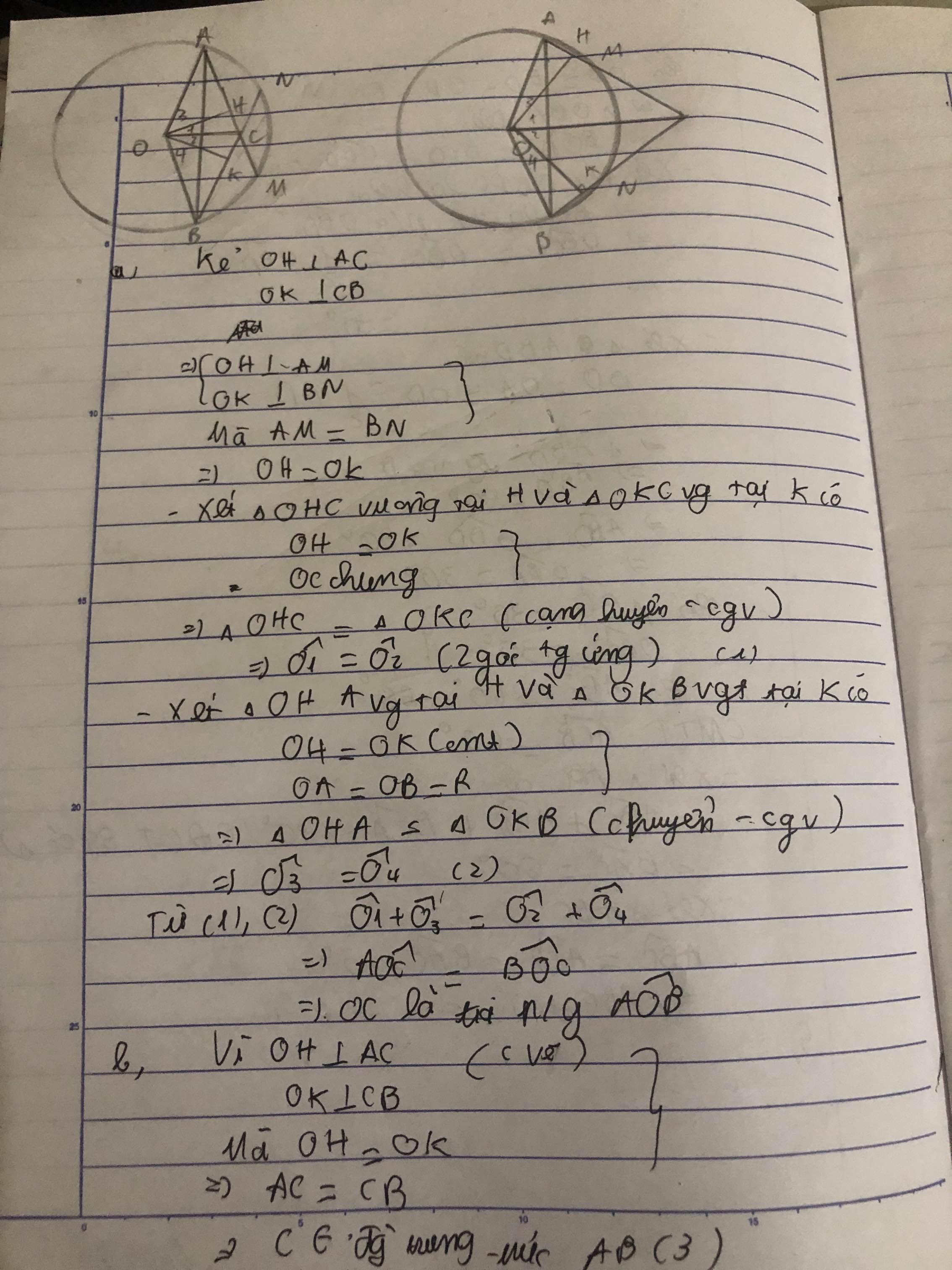
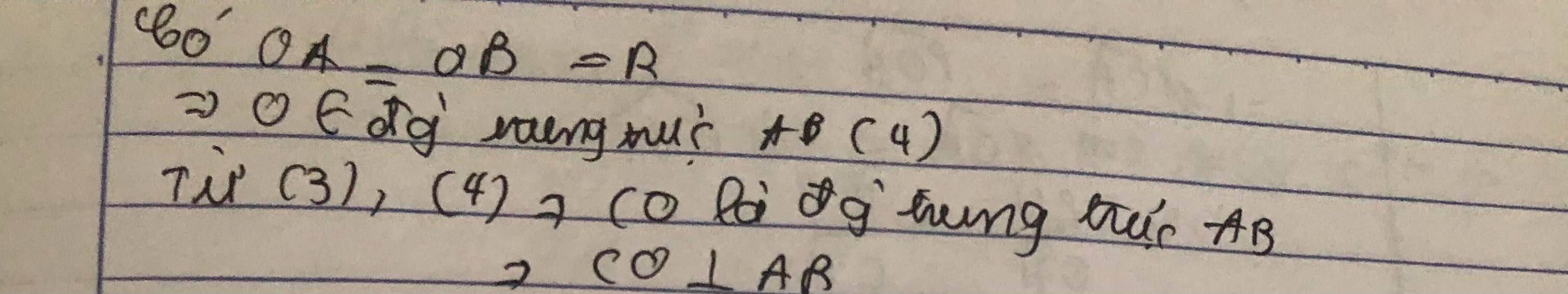
a) Xét tứ giác BIEM có
\(\widehat{IBM}\) và \(\widehat{IEM}\) là hai góc đối
\(\widehat{IBM}+\widehat{IEM}=180^0\)(\(90^0+90^0=180^0\))
Do đó: BIEM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔B,I,E,M cùng thuộc 1 đường tròn(đpcm)
b) Ta có: ABCD là hình vuông(gt)
nên BD là tia phân giác của \(\widehat{ABC}\)(Định lí hình vuông)
⇔BE là tia phân giác của \(\widehat{ABC}\)
⇔\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{IBE}=45^0\)
Ta có: BIEM là tứ giác nội tiếp(cmt)
nên \(\widehat{IBE}=\widehat{IME}\)(Định lí)
mà \(\widehat{IBE}=45^0\)(cmt)
nên \(\widehat{IME}=45^0\)
Vậy: \(\widehat{IME}=45^0\)